Ähnlichkeitsbeweis für den Satz des Pythagoras |
Beim folgenden Beweis gehen wir
gemäß der euklidischen
Methode vor.
Beweisidee:
Wir verwenden zum einen die Ähnlichkeitsbeziehungen
von
rechtwinkligen Teildreiecken des rechtwinkligen
Dreiecks ABC und zum anderen die
Flächeninhalte
von Teildreiecken des Dreiecks ABC.
Durch Kombination dieser Beziehungen
gelangen wir zum Satz des Pythagoras.
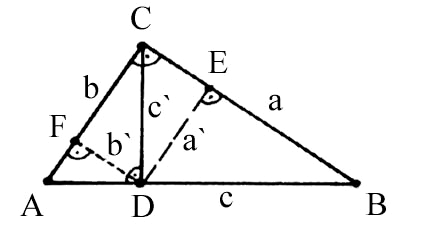 Die rechtwinkligen Dreiecke CDE und CDF sind kongruent und zu Dreieck ABC ähnlich. Deshalb gilt: a' : a = b' : b = c' : c (I) Da sich Dreieck ABC aus Dreieck ADC und Dreieck BCD zusammensetzt, können wir für die Flächenihalte schreiben: 1/2 c·c'= 1/2 a·a'+ 1/2 b·b' (II) |
Kombinieren wir (I) und (II), so ergibt sich
für die Quadratflächen über den Seiten
eines rechtwinkligen Dreiecks:
c2 = a2 + b2
Eine Übung zum Ähnlichkeitsbeweis finden Sie hier.