ergaenzungsbeweis fuer den satz des pythagoras

Beim folgenden altindischen Ergänzungsbeweis ergänzen wir das Hypotenusenquadrat bzw. die beiden Kathetenquadrate durch vier zum Ausgangsdreieck kongruente Dreiecke zu zwei Quadraten mit gleichen Seitenlänge (a+b).

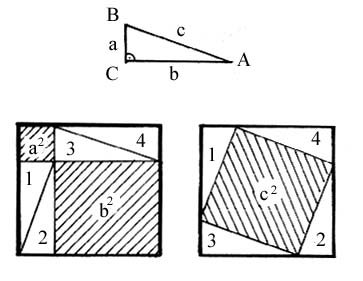Die linke Figur beinhaltet Kathetenquadrate (schraffiert) eines rechtwinkligen Dreiecks mit den Katheten a und b. Die rechte Figur beinhaltet das Hypotenusenquadrat (schraffiert) eines rechtwinkligen Dreiecks mit der Hypotenuse c.

Wir ergänzen die beiden Figuren mit vier kongruenten rechtwinkligen Dreiecken (Katheten a und b, Hypotenuse c). Da die zwei ergänzten Figuren deckungsgleich (näheres siehe hier) und damit auch flächeninhaltsgleich sind und die ursprünglichen Figuren nur durch kongruente Teilfiguren (Dreiecke ABC) ergänzt wurden, müssen auch die ursprünglichen Figuren (a^²+b^² und c^²) flächeninhaltsgleich sein.

Deshalb gilt für die Flächenquadrate über den Seiten eines rechtwinkligen Dreiecks:

Sätze	Satz des Pythagoras						Höhensatz		Kathetensatz
Beweise	Arithmeti- scher Beweis	Zerle- gungs- beweis	Ergänzungs- beweis		Ähnlich- keits- beweis	Sche- rungs- beweis	Beweis des Höhensatzes		Beweis des Kathetensatzes
Zusammen- hänge	Vom Satz des Pythagoras zum Kathetensatz			Vom Satz des Pythagoras zum Höhensatz			Vom Höhensatz zum Kathetensatz	Vom Höhensatz zum Satz des Pythagoras	Vom Kathetensatz zum Höhensatz	Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen	Umkehrung Satz des Pythagoras						Umkehrung Höhensatz		Umkehrung Kathetensatz
Prinzipien	Spezialisierung		Verallgemeinerung		Analogie