spezialisierung

Spezialisierung

Spezialfall: Gleichschenklige - rechtwinklige Dreiecke

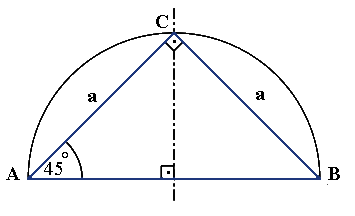Wenden wir den Satz des Pythagoras an, so gilt:

c^² = a^² + a^² = 2a^²

c = sqrt2 · a^²

Diese Beziehung gilt für jedes gleichschenklig - rechtwinkliges Dreieck.

Wegen der Irrationalität von sqrt2 kann kein gleichschenklig - rechtwinkliges Dreieck ganzzahlige Seiten besitzen.

Weitere Möglichkeit der Spezialisierung:

Pythagoreische Zahlentripel

Rechtwinklige Dreiecke, deren Seitenmaßzahlen natürliche Zahlen sind, werden oft auch "pythagoreische Dreiecke" genannt. Sind a, b, c die Seiten eines solchen, so bezeichnet man (a, b, c) als ein "pythagoreisches Zahlentripel". Nach dem Pythagorassatz und seiner Umkehrung ist also ein Tripel (a, b, c) mit a, b, c aus IN genau dann ein "pythagoreisches Zahlentripel", wenn a² + b² = c² gilt.

Sätze	Satz des Pythagoras						Höhensatz		Kathetensatz
Beweise	Arithmeti- scher Beweis	Zerle- gungs- beweis	Ergänzungs- beweis		Ähnlich- keits- beweis	Sche- rungs- beweis	Beweis des Höhensatzes		Beweis des Kathetensatzes
Zusammen- hänge	Vom Satz des Pythagoras zum Kathetensatz			Vom Satz des Pythagoras zum Höhensatz			Vom Höhensatz zum Kathetensatz	Vom Höhensatz zum Satz des Pythagoras	Vom Kathetensatz zum Höhensatz	Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen	Umkehrung Satz des Pythagoras						Umkehrung Höhensatz		Umkehrung Kathetensatz
Prinzipien	Spezialisierung		Verallgemeinerung		Analogie