analogie

Analogie

Wir bezeichnen zwei mathematische Objekte (z. B.: geometrische Figuren, algebraische Terme, Lösungsverfahren, ...) als analog zueinander, wenn sie in den Beziehungen zueinander entsprechender Elemente übereinstimmen.

Quader als räumliches Analogon zum Rechteck

Der Satz des Pythagoras kann auch interpretiert werden als eine Möglichkeit, die Diagonale d eines Rechtecks mit den Seitenlängen a und b zu berechnen:

d = sqrt(a^²+b^²).

Beim Übergang zum Quader mit den Kanten a, b, c bilden wir eine Analogie zur Raumdiagonalen des Quaders

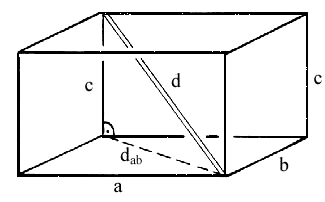Sei d_{_ab} die Diagonale in dem von den Kanten a und b aufgespannten Rechteck. Dann ist die Hypotenuse des aus d_{_ab} und c gebildeten rechtwinkligen Dreiecks gerade eine der Raumdiagonalen des Quaders. Für die Länge d gilt wegen des Pythagorassatzes folglich:

d^² = d_{_ab}^²+c^² und d_{_ab}^² = a^²+b^²

Wir erhalten die Formel zur Berechnung der Raumdiagonalen eines Quaders:

d = sqrt(a^²+b^²+c^²)

Sätze	Satz des Pythagoras						Höhensatz		Kathetensatz
Beweise	Arithmeti- scher Beweis	Zerle- gungs- beweis	Ergänzungs- beweis		Ähnlich- keits- beweis	Sche- rungs- beweis	Beweis des Höhensatzes		Beweis des Kathetensatzes
Zusammen- hänge	Vom Satz des Pythagoras zum Kathetensatz			Vom Satz des Pythagoras zum Höhensatz			Vom Höhensatz zum Kathetensatz	Vom Höhensatz zum Satz des Pythagoras	Vom Kathetensatz zum Höhensatz	Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen	Umkehrung Satz des Pythagoras						Umkehrung Höhensatz		Umkehrung Kathetensatz
Prinzipien	Spezialisierung		Verallgemeinerung		Analogie