Scherungsbeweis für den Satz des Pythagoras

 logo.jpg (12370 Byte)

Beweisidee:

Ziel unseres Beweises ist es die beiden Quadrate über den Katheten a und b eines rechtwinkligen Dreiecks in ein flächeninhaltsgleiches Quadrat über der Hypotenuse c zu verwandeln.

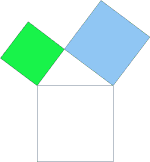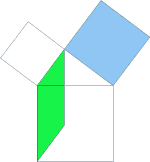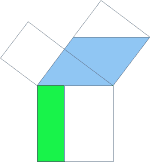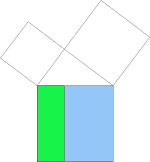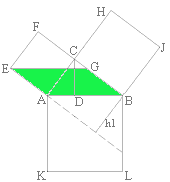
picture5.gif (13101 Byte) Wir scheren die Kathetenquadrate zu Parallelogrammen in das Dreieck ABC hinein, wobei die Scherungsachsen EA und BJ sind.

Anschließend drehen wir die Parallelogramme mit 90° um den gemeinsamen Punkt (A bzw. B).

Die Parallelogramme scheren wir zu Rechtecken in die Fläche des Hypotenusenquadrats hinein, wobei die Scherungsachsen AK und BL sind.

Sowohl bei der Scherung, als auch bei der Drehung ist der Flächeninhalt eine Invariante, deshalb ist das Quadrat über der Hypotenuse c flächeninhaltsgleich mit den beiden Quadraten über den Katheten a und b.
picture6.gif (1639 Byte)

Somit können wir schreiben:

a2+b2 = c2

Wollen Sie selbständig einen Scherungsbeweis für den Kathetensatz führen? Dann klicken Sie hier.

Sätze

 Satz des Pythagoras Höhensatz Kathetensatz

Beweise

 Arithmeti- scher Beweis Zerle- gungs- beweis Ergänzungs- beweis Ähnlich- keits- beweis Sche- rungs- beweis Beweis des Höhensatzes Beweis des Kathetensatzes

Zusammen- hänge

 Vom Satz des Pythagoras zum Kathetensatz Vom Satz des Pythagoras zum Höhensatz Vom Höhensatz zum Kathetensatz Vom Höhensatz zum Satz des Pythagoras Vom Kathetensatz zum Höhensatz Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen Umkehrung Satz des Pythagoras Umkehrung Höhensatz Umkehrung Kathetensatz

Prinzipien

 Spezialisierung Verallgemeinerung Analogie