vom hoehensatz zum satz des pythagoras

Vom Höhensatz zum Satz des Pythagoras

Beweisidee:

Aus einem gegebenen rechtwinkligem Dreieck ABC wird mit Hilfe des Thaleskreises ein Dreieck PQB konstruiert, in welchem [BC] die Rolle einer Höhe spielt. Anschließend wird der Höhensatz angewandt, woraus wir den Satz des Pythagoras erhalten.

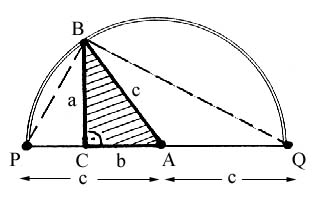P und Q sind diejenigen Punkte auf der Geraden AC, für welche gilt: |PA| = |QA| = |AB| = c.

Wegen des Satzes des Thales ist das Dreieck PQB demnach rechtwinklig mit [PQ] als Hypotenuse. Nach Konstruktion sind [PC] und [QC] die Hypotenusenabschnitte, während [BC] sich als Höhe von Dreieck PQB erweist. Die Anwendung des Höhensatzes auf das Dreieck PQB ergibt:

|BC|^² = |PC|·|QC|

also: a^² = (c-b)·(c+b)

d. h. a^² = c^² - b^², was sofort zu c^² = a^² + b^² umgeformt werden kann.

Sätze	Satz des Pythagoras						Höhensatz		Kathetensatz
Beweise	Arithmeti- scher Beweis	Zerle- gungs- beweis	Ergänzungs- beweis		Ähnlich- keits- beweis	Sche- rungs- beweis	Beweis des Höhensatzes		Beweis des Kathetensatzes
Zusammen- hänge	Vom Satz des Pythagoras zum Kathetensatz			Vom Satz des Pythagoras zum Höhensatz			Vom Höhensatz zum Kathetensatz	Vom Höhensatz zum Satz des Pythagoras	Vom Kathetensatz zum Höhensatz	Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen	Umkehrung Satz des Pythagoras						Umkehrung Höhensatz		Umkehrung Kathetensatz
Prinzipien	Spezialisierung		Verallgemeinerung		Analogie