Beweis des Kathetensatzes

Wir verwenden zur Erarbeitung des Kathetensatzes die "euklidische Methode".

Beweisidee:

Zu zeigen ist die Flächeninhaltsgleichheit vom Quadrat ACEF über der Kathete [AC] mit dem Rechteck ADGH aus der Hypotenuse und dem Hypotenusenabschnitt [AD]. Dafür genügt der Nachweis, dass Dreieck ACF (= halbes Quadrat) und Dreieck AHD (= halbes Rechteck) denselben Flächeninhalt besitzen.

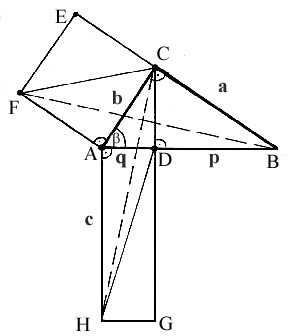Wegen BC | | AF haben die beiden Dreiecke AFC und AFB denselben Flächeninhalt (Grundlinie und Höhe der beiden Dreiecke sind identisch). Wegen CD | | AH sind auch die Dreiecke AHD und AHC flächeninhaltsgleich. Für die Dreiecke ABF und AHC gilt nun aber: |AB| = |AH|    (= Hypotenuse c) |AF| = |AC|          (= Kathete b) Winkel:  BAF = HAC    (= 90° + ß) Nach dem Kongruenzsatz SWS sind daher die Dreiecke ABF und AHC kongruent und somit flächengleich. Hieraus folgt, daß dann auch die Dreiecke ACF und AHD denselben Flächeninhalt besitzen müssen.

Also gilt im rechtwinkligen Dreieck:

Bei jedem rechtwinkligen Dreieck besitzt ein Kathetenquadrat denselben Flächeninhalt wie das Rechteck aus der Hypotenuse und dem zur betreffenden Kathete gehörenden Hypotenusenabschnitt.

a² = c·p und b² = c·q