vom satz des pythagoras zum hoehensatz

Vom Satz des Pythagoras zum Höhensatz

Beweisidee:

Wir wenden den Satz des Pythagoras am rechtwinkligen
Dreieck ABC und an dessen rechtwinkligen
Teildreiecken an und gelangen durch Addition
entsprechender Gleichungen zum Höhensatz.

Da die Teildreiecke ADC und BDC rechtwinklig sind, können wir auf diese den Satz des Pythagoras anwenden
und erhalten:

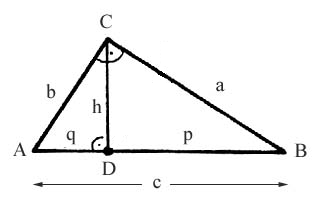b^² = q^² + h^² (*)

a^² = p^² + h^² (**)

Addition von (*) und (**) liefert:

a^² + b^² = p^² + q^² + 2h^² (I)

Ferner gilt:

a^² + b^² = c^² = (p + q)^² (II)

Setzen wir I und II gleich, erhalten wir den Höhensatz:

p^² + q^² + 2h^² = (p + q)^²

p^² + q^² + 2h^² = p^² + q^² + 2·p·q

h^² = p·q

Sätze	Satz des Pythagoras						Höhensatz		Kathetensatz
Beweise	Arithmeti- scher Beweis	Zerle- gungs- beweis	Ergänzungs- beweis		Ähnlich- keits- beweis	Sche- rungs- beweis	Beweis des Höhensatzes		Beweis des Kathetensatzes
Zusammen- hänge	Vom Satz des Pythagoras zum Kathetensatz			Vom Satz des Pythagoras zum Höhensatz			Vom Höhensatz zum Kathetensatz	Vom Höhensatz zum Satz des Pythagoras	Vom Kathetensatz zum Höhensatz	Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen	Umkehrung Satz des Pythagoras						Umkehrung Höhensatz		Umkehrung Kathetensatz
Prinzipien	Spezialisierung		Verallgemeinerung		Analogie