Zerlegungsbeweis für den Satz des Pythagoras

Beweisidee:

Wir zeigen, dass wir aus der linken Figur, deren Flächeninhalt a² + b² beträgt, durch geeignete Zerlegung und anschließender Drehung, ein flächneninhaltsgleiches Quadrat c² erhalten.

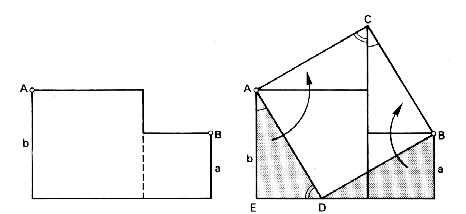Die linke Figur ist zusammengesetzt aus zwei Quadraten mit den Seiten a und b. Wir zerlegen diese Figur so, dass wir zwei kongruente rechtwinklige Dreiecke (dunkel) mit den Katheten a und b erhalten. Drehen wir diese beiden Dreiecke um 90º, so erhalten wir ein Viereck ACBD.

Aus der Kongruenz der dunklen Dreiecke und der 90º-Drehung folgern wir zunächst, daß alle vier Seiten c des Vierecks gleich lang sind. Ferner hat das Viereck wegen der Drehung bei A und B je einen rechten Winkel, und der Winkel bei C ist auch ein rechter, denn er setzt sich aus den beiden im Dreieck ADE gekennzeichneten Winkeln, die 90º betragen, zusammen. Also ist das Viereck ACBD ein Quadrat. Daher können wir für die Flächenquadrate über den Seiten der rechtwinkligen Dreiecke folgern:

a² + b² = c²

Dieser alter indischer Beweis wird auch "Stuhl der Braut" genannt.    

Eine Übung zum Zerlegungsbeweis finden Sie hier.