Vom Höhensatz zum Kathetensatz

Beweisidee:

Zu einem gegebenen rechtwinkligem Dreieck konstruieren wir mit Hilfe des Thaleskreises ein zweites rechtwinkliges Dreieck. Durch die anschließende Anwendung des Höhensatzes auf beide Dreiecke erhalten wir den Kathetensatz.

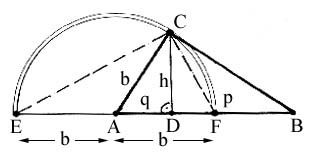Gegeben sei das rechtwinklige Dreieck ABC mit [AB] als Hypotenuse und D als Höhenfußpunkt auf  [AB]. Wir zeichnen einen Thaleskreis mit [AC] als Radius und erhalten das rechtwinklige Dreieck EFC mit [EF] als Hypotenuse, wobei D auch für dieses Dreieck Höhenfußpunkt ist. Wir wenden nun den Höhensatz sowohl auf Dreieck EFC als auch auf Dreieck ABC an und erhalten: h2 = |ED|·|DF| = (b+q)·(b-q) = b2-q2 sowie h2 = p·q Gleichsetzung ergibt:             b2 =c·q