Verallgemeinerung

Der Satz des Pythagoras gilt nicht nur für die Quadratflächen über den Seiten eines rechtwinkligen Dreiecks, sondern auch für beliebige ähnliche Figuren.

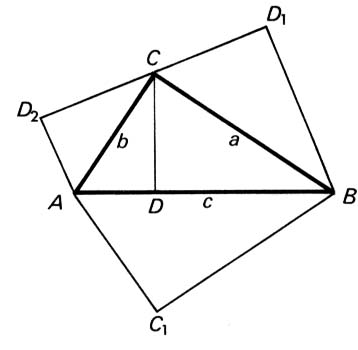Die ähnlichen Dreiecke ACD, CBD und ABC werden, wie nebenstehend dargestellt, um ihre jeweilige Hypotenuse nach außen geklappt. Wir erhalten den Zusammenhang, daß die Summe der Flächeninhalte der Dreicke über den Katheten gleich dem Flächeninhalt des Dreiecks über der Hypotenuse ist. Dieser Zusammenhang beruht auf der Ähnlichkeit der drei aufgesetzten Figuren.

Setzt man auf die Seiten des rechtwinkligen Dreiecks drei andere ähnliche Figuren F_a, F_b, F_c, (z. B. Viertel- oder Halbkreise, gleichseitige Dreiecke, Quadrate, DIN-Rechtecke,...), so sind die Verhältnisse ihrer Flächeninhalte stets gleich, nämlich wie a²:b²:c². Hieraus folgt wegen den Flächenverhältnissen c² = a²+b²:

Die Figuren F_aund F_büber den Katheten des rechtwinkligen Dreiecks sind zusammen genauso groß wie die Figur  F_c über der Hypotenuse des Dreiecks (ein bekanntes Beispiel sind die "Möndchen des Hippokrates").

Weitere Möglichkeiten der Verallgemeinerung:

• Der Kosinusatz als Verallgemeinerung des Pythagorassatzes

• Der Projektionssatz für Dreiecke als eine Verallgemeinerung des Kathetensatzes