vom kathetensatz zum hoehensatz

Vom Kathetensatz zum Höhensatz

Beweisidee:

Wir wenden den Kathetensatz am gegebenen rechtwinkligem Dreieck an und erhalten durch Gleichsetzen der Ergebnisse den Höhensatz.

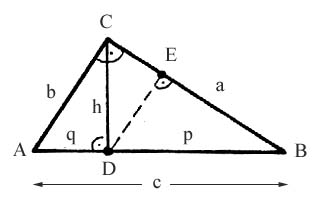Wenden wir den Kathetensatz auf das Dreieck ABC an, so gilt einerseits a^² = p·c = p·(p+q) = p^²+p·q (*). Andererseits können wir den Kathetensatz auf das Dreieck BDC anwenden, woraus sich ergibt:

h^² = a·|CE| = a·(a-|BE|) = a^²-a·|BE|

Wenden wir den Kathetensatz nochmals auf Dreieck BDC an, so gilt:

p^² = a·|BE|

dies ergibt: h^² = a^²-p^²

Mit (*) folgt dann h^² = p^²+p·q-p^² = p·q.

Sätze	Satz des Pythagoras						Höhensatz		Kathetensatz
Beweise	Arithmeti- scher Beweis	Zerle- gungs- beweis	Ergänzungs- beweis		Ähnlich- keits- beweis	Sche- rungs- beweis	Beweis des Höhensatzes		Beweis des Kathetensatzes
Zusammen- hänge	Vom Satz des Pythagoras zum Kathetensatz			Vom Satz des Pythagoras zum Höhensatz			Vom Höhensatz zum Kathetensatz	Vom Höhensatz zum Satz des Pythagoras	Vom Kathetensatz zum Höhensatz	Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen	Umkehrung Satz des Pythagoras						Umkehrung Höhensatz		Umkehrung Kathetensatz
Prinzipien	Spezialisierung		Verallgemeinerung		Analogie