Anhang zum Ergänzungsbeweis für den Satz des Pythagoras |
 |
Anhang zum Ergänzungsbeweis für den Satz des Pythagoras |
 |
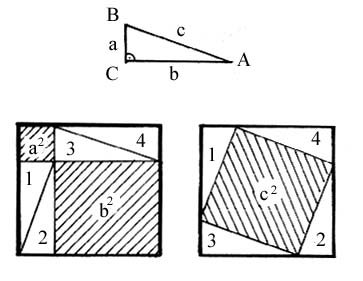 |
(1) Die linke Figur wird durch die vier kongruenten Dreiecke mit Katheten
a und b und Hypotenuse c so ergänzt, dass ein Quadrat mit der Seite a+b entsteht. (Zwei
kongruente rechtwinklige Dreiecke bilden ein Rechteck mit den Seiten a und b.) (2) Die ursprüngliche rechte Figur (schraffiertes Quadrat mit den Seiten c) wird durch kongruente rechtwinklige Dreiecke mit den Katheten a und b und Hypotenusen c ergänzt. Diese wird so ergänzt, dass die Hypotenusen c der Dreiecke an den Seiten des schraffierten Quadrats mit den Seiten c anliegen. Somit treffen die Ecke A eines Dreiecks, die Ecke B eines Dreiecks und eine Ecke des schraffierten Hypotenusenquadrats aufeinander. Da sich die Winkel bei A und B im rechtwinkligen Dreieck zu 90° ergänzen (Winkelsummensatz im Dreieck) und der Winkel des schraffierten Hypotenusenquadrats 90° ist, entsteht an dieser Stelle ein Winkel von 180°. Es entstehen hier keine zusätzlichen Ecken, bei der ergänzten Figur handelt sich also um ein Viereck. Die Seiten dieses Vierecks sind alle gleich lang, nämlich a+b und die Ecken haben einen rechten Winkel, da sich dort die rechten Winkel der ergänzten rechtwinkligen Dreiecke befinden. Also ist ein Quadrat mit den Seiten a+b entstanden. Aus (1) und (2) folgt, dass die beiden Figuren deckungsgleich sind. |