Ergänzungsgleichheit

Zwei Figuren heißen ergänzungsgleich, wenn sie sich so durch paarweise kongruente Figuren ergänzen lassen, dass die beiden entstehenden Figuren zerlegungsgleich sind.

Aus dieser Definition folgt unmittelbar, dass zerlegungsgleiche Figuren auch ergänzungsgleich sind.

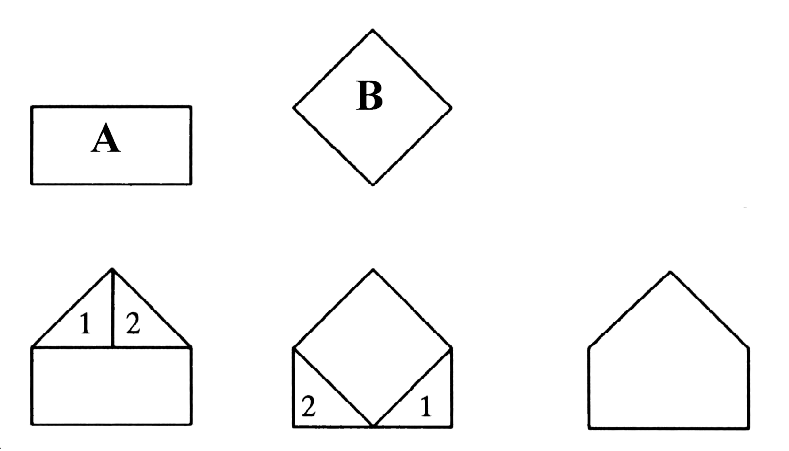Bei diesem Beispiel haben wir die Figuren A und B jeweils mit kongruenten Dreiecken ergänzt und somit zwei zerlegungsgleiche Figuren erhalten. Da die ergänzten Figuren laut Definition zerlegungsgleich sind und die ursprünglichen Figuren nur durch kongruente Teilfiguren ergänzt wurden, müssen auch die ursprünglichen Figuren zerlegungsgleich sein.

Um zu zeigen, dass Zerlegungsgleichheit und Ergänzungsgleichheit äquivalente Begriffe sind, benötigt man einen expliziten Beweis (hier ohne Beweis).

Mit Hilfe dieser Erkenntnis und deren aus Kapitel Zerlegungsgleichheit können wir formulieren:

Ergänzungsgleiche Figuren sind flächeninhaltsgleich.