Zerlegungsgleichheit |
 |
Zerlegungsgleichheit |
 |
Betrachten wir zwei kongruente Figuren, so ist uns klar (kongruent = deckungsgleich), dass beide flächeninhaltsgleich sind.
Wann sind zwei inkongruente Figuren flächeninhaltsgleich?
Ist es möglich zwei Figuren A und B in endlich viele Teilfiguren A1, A2, ...An bzw. B1, B2,...Bn so zu zerlegen, dass gilt:
A1 ist kongruent zu B1
A2 ist kongruent zu B2
:
An ist kongruent zu Bn
dann sind Figuren A und B zerlegungsgleich bzw. flächeninhaltsgleich.
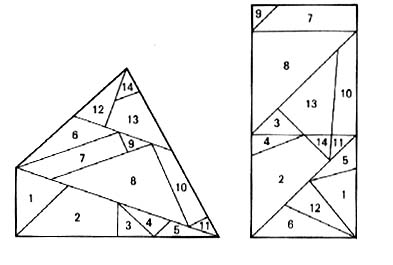 |
Die nebenstehende Figur zeigt ein Beispiel zweier zerlegungsgleicher Figuren. Die entsprechenden kongruenten Teilfiguren sind durch gleiche Ziffern gekennzeichnet. |