Scherung

Das Prinzip der Scherung erkennt man an folgendem Modell.
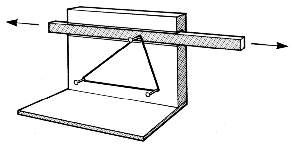bild56.gif (18714 Byte)

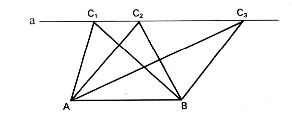
Übertragen auf die geometrische Figur entsprechen die Punkte C1, C2, und C3 der Dreiecke ABCn verschiedenen Positionen des Nagels in der Führungschiene, wobei a || AB ist.

bild55.gif (9775 Byte)

Die Flächentreue der Scherung sehen wir daran, dass die Flächeninhalte der Dreiecke ABC1, ABC2 und ABC3 gleich sind, denn A=1/2·|AB|·h (h:=Abstand von AB zu a)

 

Abbildungsvorschrift der Scherung


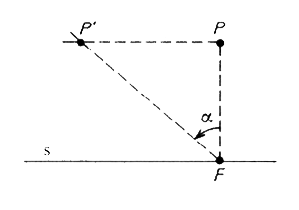bild57 Kopie.gif (4655 Byte)

  • Jeder nicht auf der Scherungsachse s liegende Punkt P wird so auf einen Bildpunkt P`abgebildet, daß gilt:

              P` liegt auf einer Parallelen zu s durch P,

              Winkel PFP` ist Scherungswinkel.

               (F ist Fußpunkt des Lotes von P auf s)

  • Jeder auf der Scherungsachse s liegende Punkt F wird auf sich abgebildet, ist also Fixpunkt.

 

Sätze

 Satz des Pythagoras Höhensatz Kathetensatz

Beweise

 Arithmeti- scher Beweis Zerle- gungs- beweis Ergänzungs- beweis Ähnlich- keits- beweis Sche- rungs- beweis Beweis des Höhensatzes Beweis des Kathetensatzes

Zusammen- hänge

 Vom Satz des Pythagoras zum Kathetensatz Vom Satz des Pythagoras zum Höhensatz Vom Höhensatz zum Kathetensatz Vom Höhensatz zum Satz des Pythagoras Vom Kathetensatz zum Höhensatz Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen Umkehrung Satz des Pythagoras Umkehrung Höhensatz Umkehrung Kathetensatz

Prinzipien

 Spezialisierung Verallgemeinerung Analogie