anhang zum arithmetischen Beweis

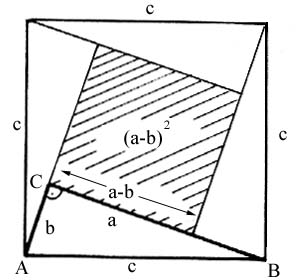Warum passen die vier kongruenten Dreiecke wie in der Figur in das Quadrat?

Die Dreiecke kann man genau auf die Seiten des Quadrats setzen, da deren Hypotenusen c ihnen entsprechen. Da die Dreiecke bei C einen Winkel von 90° besitzen, müssen die beiden anderen Winkel zusammen (Winkelsummensatz i. Dreieck) auch 90° ergeben. Da der Winkel bei A und der Winkel bei B zweier Dreiecke zusammen 90° ergeben, kann man diese beiden Ecken genau in die Ecke eines Quadrats (Winkel 90°)einpassen. Die vier Dreiecke sind kongruent, deshalb gilt diese Anordnung für alle vier.

Warum ist der so entstehende freie Platz ein Quadrat mit den Seiten a-b?

Da die kongruente Dreiecke wie oben erklärt in das Quadrat mit den Seiten c eingepaßt werden können, schließt sich an die Seiten a der Dreiecke eine freie Fläche und die Seiten b der benachbarten Dreiecke an. Also liegt für die Länge a-b ein freier Platz an den Seiten a des Dreiecks an. Da die Dreiecke kongruent sind, hat der freie Platz auf allen vier Seiten die Länge a-b. Die Ecken des freien Platzes bilden einen Winkel von 90°, da der rechte Winkel der Dreiecke bei C und der Winkel der Ecken des freien Platzes sich zu 180° ergänzen (Summe zweier Nebenwinkel ergibt 180°).

Sätze	Satz des Pythagoras						Höhensatz		Kathetensatz
Beweise	Arithmeti- scher Beweis	Zerle- gungs- beweis	Ergänzungs- beweis		Ähnlich- keits- beweis	Sche- rungs- beweis	Beweis des Höhensatzes		Beweis des Kathetensatzes
Zusammen- hänge	Vom Satz des Pythagoras zum Kathetensatz			Vom Satz des Pythagoras zum Höhensatz			Vom Höhensatz zum Kathetensatz	Vom Höhensatz zum Satz des Pythagoras	Vom Kathetensatz zum Höhensatz	Vom Kathetensatz zum Satz des Pythagoras
Umkehrungen	Umkehrung Satz des Pythagoras						Umkehrung Höhensatz		Umkehrung Kathetensatz
Prinzipien	Spezialisierung		Verallgemeinerung		Analogie