Differenzierung mit GeoGebra am Beispiel der Flächenberechnung
Aus GeoGebra-Institut Landau (RLP)
Flächeninhalt vom Rechteck, Parallelogramm und rechtwinkliges Dreieck
Zielgruppe: Orientierungsstufe
Methode: Lerntempoduett.
Eine Beschreibung der Methode finden Sie auf den Seiten von Landesakademie für Fortbildung und Personalentwicklung an Schulen (BW)[1].
| Im Unterricht: | |
|---|---|
1. Aufgabe: Flächeninhalt Rechteck
|
|
2. Aufgabe:Rechtek und Parallelogramm
|
|
3. Aufgabe: Rechteck und Dreieck
|
Flächeninhalt vom Kreis
Zielgruppe: Mittelstufe
Methode: Gruppenpuzzle.
Eine Beschreibung der Methode finden Sie auf den Seiten von Landesakademie für Fortbildung und Personalentwicklung an Schulen (BW)[2].
| Gruppe | Datei |
|---|---|
| 1. Gruppe: Eingeschriebene Vielecke Die Kreisfläche wird durch eingeschriebene regelmäßige Vielecke genähert. Erstellen Sie eine Datei, wie rechts. Hier finden Sie eine grobe Konstruktionsbeschreibung: Datei:Anleitung- Kreis nähern von innen.pdf. ... und zur Lösung geht es hier entlang: Flächeninhalt eines Kreises - Eingeschriebene Vielecke |
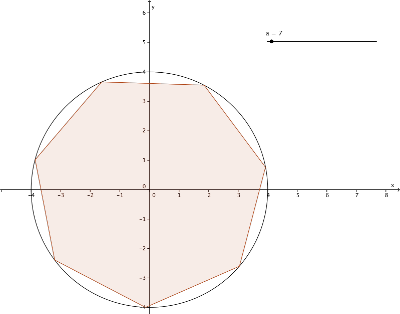
|
| 2. Gruppe: Umgeschriebene Vielecke Die Kreisfläche wird durch umgeschriebene regelmäßige Vielecke genähert. Erstellen Sie eine Datei, wie rechts. Sie finden eine grobe Konstruktionsbeschreibung im Briefumschlag. |
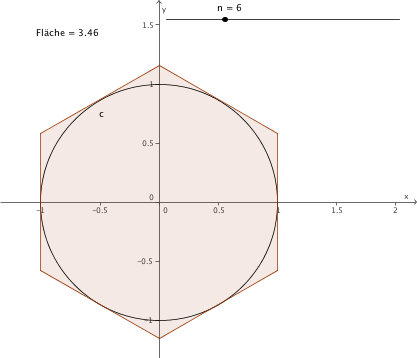
|
| 3. Gruppe: Die Monte-Carlo-Methode Die Mitglieder dieser Gruppe werden mit Listen arbeiten. Erfahrungen mit einer Programmiersprache erleichtert die Arbeit, ist jedoch keine Voraussetzung für das Gelingen. Für diejenigen, die Unterstützung haben möchten, haben wir das Konstruktionsprotokoll hier Datei:Anleitung Monte-Carlo-Methode.pdf hochgeladen. |
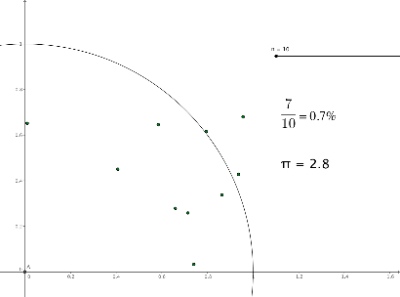
|
| 4. Gruppe: Recherche bei GeoGebraTube suchen Sie nach geeigneten Dateien bei GeoGebra Tube [3] und nehmen Sie Stellung zu deren Einsatz im Unterricht. Denken Sie daran, dass GeoGebra Tube mehrsprachig ist, benutzen Sie Suchbegriffe in mehreren Sprachen. |
|

