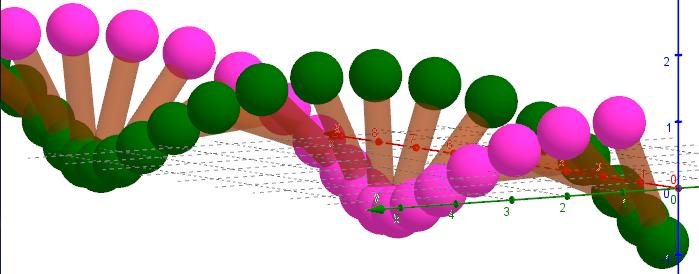
3D-Veranschaulichung mit GeoGebra (Balk)
Das folgende Material ist für die Fortbildungsveranstaltungen des Pädagogischen Landesinstitut in Rheinland Pfalz mit GeoGebra 5.0 erstellt worden. Es handelt sich hier um sogenanntes "graues Material". Das heißt, dass obwohl wir die Unterlagen sorgfältig geprüft und aktualisiert haben, wir keinen Anspruch auf Fehlerfreiheit erheben möchten. Dies würde unsere Möglichkeiten übersteigen.
3D-Vorlagen zur Kopie freigegeben
Sie sollten bei den ggb-Dateien zunächst die 3D-Version geöffnet haben, bevor Sie sie benutzen. Die unten angegebenen Links benutzen Sie also, um die entsprechenden Dateien auf Ihren Rechner zu laden, um sie später erst zu öffnen.
Das Programm mit den vielen bunten Würfeln,
bei dem die Schüler die 3D-Ansicht nutzen können, um aus den Würfeln z.B. einen Torbogen zu erstellen, ist hier: [[1]]
Und die Helix, die man mit dem Schieberegler aufdrehen kann,
ist hier erhältlich: [[2]]
Ethan und seine Konformationen

ist als ggb-Datei hier zu haben: [[3]]
Mein youtube-video, das einen Eindruck von dem 3D-Effekt gibt, wenn man eine rot-cyan-farbige 3D-Brille aufsetzt, ist in [[4]] zu sehen.
Wünsche der Teilnehmer für die Zukunft
Unsere Teilnehmer haben folgende Verbesserungsvorschläge / Wünsche für die zukünftigen GeoGebra-Versionen gemacht:
1) Ebenen in Großbuchstaben
Das gilt auch schon für GeoGebra ohne 3D-Version.
2) Eine Möglichkeit, Ebenen in der Koordinatenform einzugeben, z.B. 2 x + 3 y +z =2
3) Bei elementaren Objekten wie Kreisen und Ebenen sollte es einfach sein, eine Gleichung der Schnittkurve anzugeben. Das ist momentan noch nicht verwirklicht worden. Auch Kegelschnitte sollten dann eigentlich recht einfach als Gleichung angebbar sein, denn das ist ja sogar das Markenzeichen von GeoGebra.
4) Objekte sollten in der Algebraansicht auswählbar sein, denn so könnte man die Werkzeuge der 3D-Ansicht präziser nuzen.
PREZI-Präsentation
Da die PREZI zu groß ist, um sie als Ganzes hier abzuspeichern, habe ich den Link zu ihr freigegeben [[5]]
Neuigkeiten zu 3D-GeoGebra
Hier werden die Neuigkeiten, z.B. neuere Versionen zum Offline-Betrieb bekanntgegeben.
Die neueste online-Version hat m.E. die Nr. 4.9.21 (Java 1.6.0_29, 492MB, MPReduce .016) 08 May 2012
Ich habe es geschafft, eine offline-Version aus der Version des Russen zu erstellen, die durch dessen update-Befehl auch
die neuesten ggb-files enthält.
Diese übernahm allerdings dann die settings des Russen, so dass die ganze Seite ohne die
"extrude to pyramid or cone" und ausserdem auf russisch dargestellt wurde, und die Fenster waren seltsam angelegt,
die üblichen Befehle die bei der onlineversion http://www.geogebra.org/webstart/5.0/geogebra-50.jnlp gewohnt waren,
tauchten nicht auf.
Nun habe ich die .bat datei des Russen verändert, und seine settings daraus gelöscht. Es funktioniert! Kann aber auch deshalb sein, weil ich zuhause ja online bin, möglicherweise ist diese Version also gar nicht offline-tauglich. Also noch nicht zu früh freuen! Sieht aber gut aus, funktioniert bei mir zu hause auch ohne Internetanschluss.
Damit habe ich eine funktionsfähige 3D-GeoGebra-Version erschaffen, die ich am Mo.14.5.2012 bei uns an der Schule testen werde, ob sie wirlich offline auch funktioniert. Wenn sie funktioniert, melde ich mich wieder hier.
Ok, habe an zwei neueren Rechnern in der Schule getestet, funktioniert! --S.Balk 18:37, 24. Mai 2012 (CEST) Prima, das funktioniert an allen Rechnern der Schule. Ich würde diese 5.0-Version gerne in das allgemeine GeoGebra-Forum hochladen für Beta-Versionen im deutschsprachigen Raum, aber ich kann mich nicht einloggen, irgendetwas stimmt da mit dem register-login nicht.--S.Balk 09:33, 20. Jun. 2012 (CEST)
Spezielle Fragen und Antworten
bei Apple potenzieren
F: Mit einem Apple kann man nicht die ^ Taste benutzen, um zu potenzieren, z.B. x hoch 5 ist ja sonst x^5. Wie gibt man die Potenz bei Apple ein?
A: Wir haben vorgeschlagen: x**5 Beim PC funktioniert jedenfalls auch dieser Befehl.
A: Bei meinem Apple funktioniert's mit der Taste ^ . Ich muss allerdings die Taste für den Exponenten zweimal betätigen: Für x^5 drücke ich die Taste 5 zweimal. (Bem.: Katalin Retterath)
Rotationskörper
F: Wie kann man Rotationskörper darstellen?
A: Man gibt im Eingabefenster erst einmal die Funktion ein, die man rotieren lassen will, z.B.:
f(x)= 1+sin(x)/2 und danach:
Oberfläche[u, cos(v) f(u), sin(v) f(u), u, 0, 7, v, 0, 2 Pi] Das ergibt die Mantelfläche des Rotationskörpers, der x-Bereich von 0 bis 7, eine volle 360Grad-Drehung also von 0 bis 2 Pi.
Der Oberfläche-Befehl ist auch für anderes nützlich, allgemein lautet er:
Oberfläche[ <Expression>, <Expression>, <Expression>, <Parameter Variable 1>, <Start Value>, <End Value>, <Parameter Variable 2>, <Start Value>, <End Value> ]
Für die Arbeit mit Schülern würde ich empfehlen, eine Datei mit Schiebereglern a und b sowie dem schon eingegebenen f(x)= 1+sin(x)/2 Oberfläche[u, cos(v) f(u), sin(v) f(u), u, a, b, v, 0, 2 Pi]
vorzugeben, das die Schüler benutzen können und sie können darin einfach die Funkton f abändern und mit den Schiebereglern die Grenzen einstellen. Eine entsprechende Datei habe ich zum download vorbereitet: [[6]]