2 - Die Herren Bezier und de Casteljau und ihre Kurven
Pierre Bezier und Paul de Casteljau
Pierre Bezier
Aus Wikipedia:
"Pierre Étienne Bézier ... (* 1. September 1910 in Paris; † 25. November 1999) war ein französischer Ingenieur von Arts et Métiers ParisTech.
In den 1960er Jahren beschrieb er die Bézierkurve, die bei seinem damaligen Arbeitgeber Renault zur Gestaltung von Karosserieformen genutzt wurde...
Die Bézierkurve hat sich als äußerst praktisches Verfahren zur Beschreibung von Kurven bei Computerprogrammen erwiesen. Bézierkurven werden von relativ wenigen „Knotenpunkten“ aufgebaut, in denen als „Zusatzinformation“ die Art des Knotens, zum Beispiel symmetrisch oder spitz, sowie Richtung und „Richtungsintensität“ der abzweigenden Linien angegeben werden."
Paul de Casteljau
Aus Wikipedia:
"Paul de Faget de Casteljau studierte Mathematik und Physik an der École normale supérieure in Paris, leistete seinen Wehrdienst im Algerienkrieg ab und begann 1958 als Physiker bei Citroën, in der Groupe Détermination Mathématique des Carrosseries. Von dort aus wurden beim französischen Patentamt Institut national de la propriété industrielle (INPI) de Casteljaus grundlegende Dokumente zur Modellierung von Kurven und Flächen mit Splines hinterlegt. Ende der 1980er Jahre gelang ihm die Verbindung von Bézier- und B-Spline-Technik durch das Blossoming. Seit Anfang der 1990er Jahre ist er im Ruhestand und hat sich darin zuletzt mit Quaternionen und metrischer Geometrie beschäftigt."
Bezierkurven
Die Bezierkurven bestechen durch ihr Eleganz und weich Übergänge. Sie sind in den 1950er-60er Jahren von Pier Bezier und Paul de Casteljau entwickelt worden, wobei Paul de Casteljau von seinem Arbeitgeber, Citroën zur Geheimhaltung verpflichtet wurde.
Konstruktion
Konstruktion mit der De-Casteljau-Algorithmus
Gegeben:
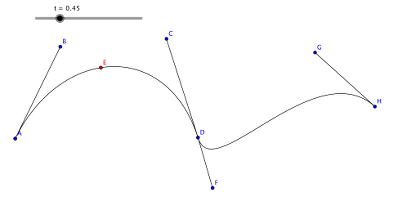
Gegeben sind vier Punkte A, B, C und D sowie ihre Verbindungsstrecken.
Idee:
Alle gegebene (AB, BC und CD) und neu entstandene Strecken (EF, FG, GH und HI) werden im gleichen Verhältnis geteilt. Dieses Verhältnis wird vom t bestimmt.
Wenn der Wert von T verändert wird, verändert sich auch die Position vom Punkt J. Die Kurve, die J "auf das Blatt gezeichnet" ist die Bezierkurve, die zu den Punkten A, B C und D gehört.
Konstruktionsan:
Die Konstruktion können Sie Schritt für Schritt verfolgen, wenn Sie diesem Link auf die Seite von GeoGebraTube folgen.
Bezierkurven aneinander fügen
Bezier-Werkzeug erstellen
Animierte Bewegungen folgen Bezier-Splines (lückenlos aneinander fügte Bezieh-Kurven). Damit nicht jeder Kurvenabschnitt mühsam konstruiert werden muss, ist es sinnvoll ein Werkzeug zu erstellen, das Bezier-Kurven automatisch konstruiert.
Öffnen Sie ihre Datei mit der Basiskonstruktion und erstellen Sie das Werkzeug, wie auf der Bildstrecke beschrieben:
1. Wählen Sie in der Menüleiste Werkzeuge / Neues Werkzeug erstellen
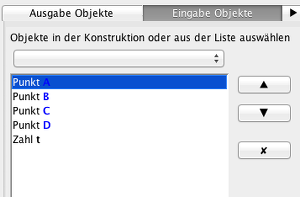
2. Sie können aus einer Liste die Eingabeobjekte aussuchen.
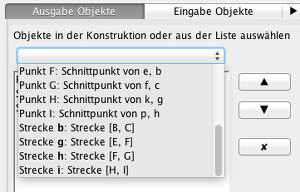
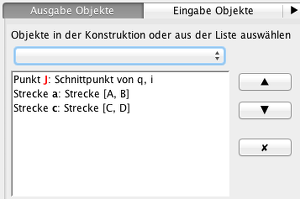
3. Bestimmen Sie im nächsten Schritt die Ausgabeobjekte, wie auf dem Bild.
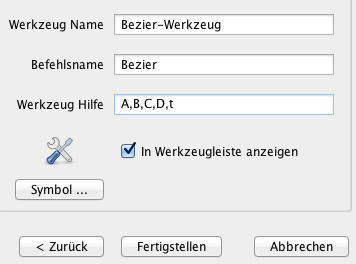
4. Geben Sie im letzten Fenster Ihrem Werkzeug einen sinnvollen Namen. Der Werkzeug-Hilfe zeigt Ihnen bei der Nutzung, in welcher Reihenfolge Sie die Eingabeobjekte angeben müssen.
Objekte entlang Bezier-Splines führen
1. Erstellen Sie einen Bezier-Spline aus zwei Kurvenstücken:
- Legen Sie einen Schieberegler "t" mit folgenden Eigenschaften an:
- Benutzen Sie den gerade erstellten Bezier-Werkzeug um zwei Kurvenstücke zu erstellen.
- 1. Kurvenstück: Nehmen Sie vier beliebige Basispunkte und t als Parameter.
- 2. Kurvenstück: Nehmen Sie als erster Basispunkt für diesen Kurvenstück den letzten Basispunkt des ersten Kurvenabschnitts.
- Nach drei beliebigen weiteren Bisspunkten geben Sie als Parameter t-1 an.
- 3. Benutzen Sie für die Anzeige der Bezier-Kurven ggf. den Befehl "Ortslinie" in der Eingabezeile.
- Mit Hilfe der angezeigten Strecken können Sie die Kurven so verformen, dass sie möglichst sanft ineinander übergehen.
2. Bild einbinden
- Speichern Sie das Bild eines Balles auf ihrem Computer (z.B. von Openclipart.org) oder laden Sie das Bild links herunter.
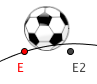
- Definieren Sie einen neuen Punkt, indem Sie in die Eingabezeile E2=(x(E)+1,y(E)) eingeben. (E ist der Punkt, der die Bezierkurve "zeichnet")
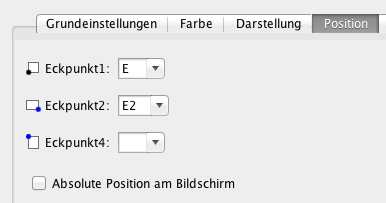
- Fügen Sie das Bild des Balles ein (Hilfe) und stellen Sie die Position (Rechtsklick auf das Bild / Eigenschaften / Position) wie auf dem Bild ein.
- Verfahren Sie auf ähnlicher Weise mit dem Punkt des zweiten Kurvenstückes.
Animation starten
- Blenden Sie alle störende Objekte aus und starten Sie die Animation (Rechtslich auf den Schieberegler, Animation starten).