1 - Einfache Animationen
Der hüpfende Ball
Grundidee
Wir lassen einen Punkt entlang eines Parabel wandern. GeoGebra gibt uns die Möglichkeit ein Bild eines Balles an diesem Punkt zu binden. Wenn die nicht benötigte Konstruktionselemente ausgeblendet werden, sieht es so aus, als ob der Ball "von alleine" hüpfen würde.
Vorbereitung
Laden Sie das Bild (50px) eines Balles auf Ihren Rechner , z.B. von den Seiten von openclipart.org oder laden Sie dieses Bild herunter: 
Konstruktion
Sie können die Konstruktion Schritt für Schritt auf GeoGebraTube verfolgen.
Mehrere Sprünge
In diesem Abschnitt werden wir versuchen den Ball mehrere Sprünge springen lassen.
Um Ihre Arbeit zu erleichtern können Sie eine Vorlage von GeoGebraTube hier herunterladen oder die Datei mit der Onlineversion von GeoGebra (hier) konstruieren.
Selbstverständlich können Sie auch mit ihrem GeoGebra-Software ohne Vorlage weiterarbeiten - in diesem Fall fehlt Ihnen aber das Werkzeug: Parabel-2.
Parabeln anpassen
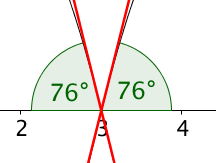
Natürlich können die Parabeln nicht willkürlich angelegt werden.
Die Physik lehrt uns: Der Aufprallwinkel des Balles ist gleich mit dem Winkel, wie der Ball wieder "wegspringt".
Abnehmender Höhe
Der Ball verliert beim jeden Aufprall eine bestimmte Prozent seiner Energie, dadurch auch die Höhe des nächsten Sprunges. Wie viel das genau ist, hängt von der Beschaffen seit von Ball und Boden ab.
Legen Sie eine Reihe von Parabeln an, deren Scheitelpunkt immer 20% niedriger als der vorige liegt. Arbeiten, wie bei "Mehrere Sprünge" und "Parabeln anpassen" beschrieben weiter.
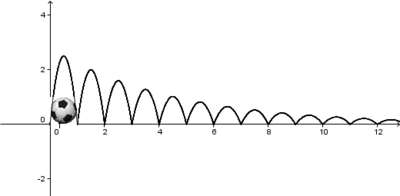
Lösung mit einer abschnittsweise definierten Funktion
![]() Eine sehr elegante, wenn auch (inhaltlich) nicht ganz einfache Lösung. Die Idee und Umsetzung entstand auf der Fortbildungsveranstaltung "Mathematik und Medien" in April 2015.
Eine sehr elegante, wenn auch (inhaltlich) nicht ganz einfache Lösung. Die Idee und Umsetzung entstand auf der Fortbildungsveranstaltung "Mathematik und Medien" in April 2015.
Konstruktionsprotokoll
| Zahl t | ||
| Zahl a | floor(t) | |
| Funktion f | f(x) = Wenn[a ≤ x ≤ a + 1,-(10 (0.8^a)) (x - a) (x - a - 1)] | |
| Punkt A | (t, f(t)) | |
| Bild Bild1 | ||
| Punkt B | (x(A) + 1, y(A)) |
Bemerkungen:
- floor(t) schneidet die Dezimalstellen von t ab
- in Zeile 3 wird ein Funktionenschar in Abhängigkeit von a definiert