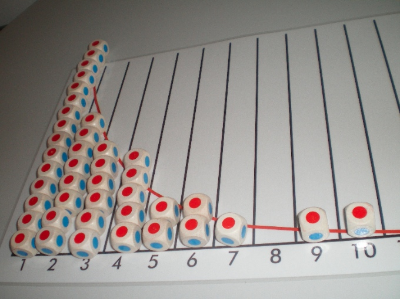
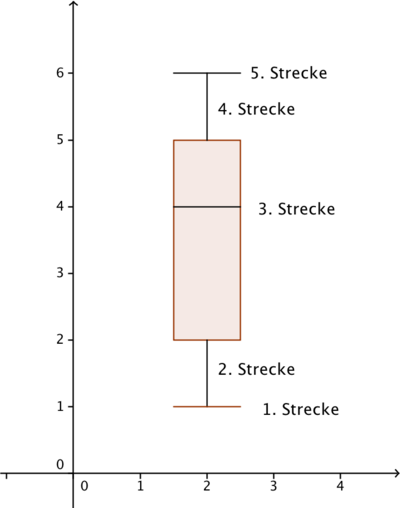Rote Würfel raus
§ |
Das folgende Material ist für die Fortbildungsveranstaltungen des Pädagogischen Landesinstitut in Rheinland Pfalz mit GeoGebra 4.0 erstellt worden. Es handelt sich hier um sogenanntes "graues Material". Das heißt, dass obwohl wir die Unterlagen sorgfältig geprüft und aktualisiert haben, wir keinen Anspruch auf Fehlerfreiheit erheben möchten. Dies würde unsere Möglichkeiten übersteigen. |
Experimentbeschreibung
Auf dem Tisch liegen 50 Würfel, bei denen zwei Seiten rot gefärbt sind. Mit all diesen Würfeln wird gewürfelt. Manche zeigen eine rote Fläche. Diese Würfel werden aneinander in die erste Spalte gelegt. Mit den übrigen Würfeln wird noch einmal gewürfelt. Diesmal werden die roten Würfel in die zweite Spalte gelegt. Das Experiment wird so lange wiederholt, bis alle Würfel einsortiert sind.
Datenbearbeitung mit GeoGebra ...
... in der SI ...
Link zu der GeoGebra-Datei: [1]
Wenn die Boxplots anstatt waagerecht, senkrecht gezeichnet werden, wird eine andere Stärke deutlich.
Wir werten "Messreihen" mit Boxplots aus.
Damit die Experimentierreihen vergleichbar sind, wurde mit n = 50; 34; 23; 16; 11 und 8 Würfeln je 10-mal gewürfelt und die Anzahl der roten Würfeln notiert.
Die Boxplots wurden aus diesen 10er-Reihen erstellt.
Wenn wir nun die Funktion suchen, die durch die Messreihe definiert wird, ist der Verlauf auf dem ersten Blick erkennbar. Für die Schülerinnen und Schüler der 7-8. Klassen reicht es aus zu erkennen, das die Kurve dem Bild ähnelt, das beim Legen der Würfeln entsteht. Fortgeschrittene GeoGebra-Benutzer können es versuchen ein geeignetes Foto der Würfeln als Hintergrund einzubinden.
In den höheren Klassen kann man versuchen eine geeignete Funktionsgleichung zu finden.
Da GeoGebra keine Möglichkeit bietet Boxplots senkrecht zu zeichnen oder waagerecht gezeichnete Boxplots zu drehen oder spiegeln, ist es notwendig ein eigenes Werkzeug für diese Aufgabe zu erstellen.
... in der SII ...
Link zu der GeoGebra-Datei: [2]
Ein Blick hinter den Kulissen
Benutzerdefiniertes Werkzeug: BoxplotVert
Vorbereitung
Erstellen Sie eine neue GeoGebra Datei mit
- einer Liste "L" von Rohdaten und
- bestimmen Sie die notwendige Kenngrößen:
- ma = Maximum,
- mi = Minimum,
- me = Median,
- uq = unteres Quartil (Q1),
- oq = oberes Quartil (Q3)
- Außer diesen Kenngrößen benötigen wir noch zwei weitere Zahlen:
- xA für den x-Abstand: Diese Zahl gibt an, wie weit der Boxplot von der y-Achse horizontal entfernt ist.
- xS für die x-Skalierung: Der Boxplot wird doppelt so "dick" sein, wie diese Zahl.
Vertikalen Boxplot zeichnen:
Wir kommen nicht drumherum: wir müssen einmalig den Boxplot aus seinen Bestandteilen zusammenbauen.
| Schritt | Was ? | Wo? | Wie? |
|---|---|---|---|
| 1 | Strecken Zeichnen | Eingabezeile | Alle Strecken müssen einzeln gezeichnet werden:
|
| 2 | Box Zeichnen | Eingabezeie | Verwenden Sie das Befehl "Vieleck" und geben Sie die vier Eckpunkte nacheinander im Umaufsinn ein. |
Werkzeug erstellen und speichern
| Schritt | Was ? | Wo? | Wie? |
|---|---|---|---|
| 1 | Dialog aufrufen | Menüleiste | Werkzeuge / Neues Werkzeug erstellen |
| 2 | Ausgabeobjekte Definieren | Auswahlliste | Die 5 Strecken und das Viereck müssen ausgewählt werden. Klicken Sie anschließend auf "Weiter". |
| 3 | Eingabeobjekte definieren | Es sollen xA, xS und L übrig bleiben. Alle andere Werte können aus diesen Eingaben berechnet werden. Klicken Sie anschließend auf "Weiter". | |
| 4 | Werkzeugname = Befehlsname angeben | Dialogfenster | Geben Sie einen sprechenden Namen ein, z.B. BoxplotVert. Wenn Sie es möchten, können Sie auch einen Hilfetext eingeben. Klicken Sie anschließend auf "Fertigstellen". |
| 5 | Werkzeug ausprobieren | Werkzeugleiste | Rufen Sie das neue Werkzeug auf. Geben Sie zwei Zahlen ein und klicken Sie anschließend auf eine Liste im Algebra-Ansicht. |
| 6 | Werkzeug speichern | Menüleiste | Dieses Werkzeug steht vorerst nur in dieser Datei zur Verfügung. Damit Sie es auch in anderen Dateien verwenden können, müssen Sie es speichern. Am Besten legen Sie irgendwo einen Ordner für Ihre eigenen Werkzeuge an, damit Sie sie schnell wieder finden. Werkzeuge / Werkzeuge verwalten / Speichern unter ... |
Werkzeug in eine neue Datei einbinden
| Schritt | Was ? | Wo? | Wie? |
|---|---|---|---|
| 1 | Öffnen Sie eine neue Datei ... | Menüleiste | ... und zeichnen Sie etwas. |
| 2 | Werkzeug einbinden | Menüleiste | Klicken Sie auf Datei / Neu. Speichern Sie Ihre Datei nicht. Suchen Sie Ihr Werkzeug-Ordner und öffnen Sie das eben erstellte Werkzeug. Wenn Sie alles richtig gemacht haben, erscheint jetzt das neue Werkzeug in der Werkzeugleiste und Ihre Zeichnung bleibt erhalten. |
Werkzeug aufrufen
Sie haben zwei Möglichkeiten das eben erstellte Werkzeug aufzurufen:
Sie können das Symbol aus der Werkzeugleiste verwenden oder den Namen des Werkzeuges in die Eingabezeile eintippen.
Trendlinien
Im Unterricht
In der S I:
Einige Hinweise für den Unterricht haben wir schon bei den Kapiteln "Experimentbeschreibung" und der "Datenbearbeitung mit GeoGebra" gegeben. Es ist für die Schülerinnen und schüler immer wieder überraschend, dass die vorgezeichnete Linie immer wieder entsteht (vergl. Bild).
Messreihen kann Ihnen der Physikunterricht liefern: Treten Sie mit dem Physiklehrer der Klasse schon am Anfang des Schuljahres in Verbindung, damit Sie auf Messergebnisse zurückgreifen können. Auch im Mathematikunterricht kann experimentiert werden: lassen Sie z.B. 10-20-30-40-... Bohnen wiegen.