GeoGebra als CAS - Speyer 2015

Skript zur Fortbildung als PDF verfügbar!

Informationen zu einigen technischen Fragen, die meinen Unterricht betrafen, am Ende der Seite. Ebenso angefragte GeoGebra-Dinge.

Hinweis: Alle hier vorgestellten Arbeitsblätter sind in einem GeoGebraBook auf GeoGebraTube gesammelt worden. Dieses ist über diesen Link erreichbar.

Wer noch nicht weiß was GeoGebraTube und ein GeoGebraBook ist: GeoGebraTube ist eine Online-Sammlung von GeoGebra-Arbeitsblättern. Das Design ist darauf ausgerichtet, dass die Bedienung möglichst einfach ist und man ein für Schüler vorbereitetes Arbeitsblatt möglichst schnell hochladen kann. Deshalb gibt in den aktuellen GeoGebra-Versionen im Datei-Menü den Befehl "Teilen", wodurch man mit einem Klick in den Hochlade-Dialog kommt. Neben dieser Bequemlichkeit hat GGT auch das Ziel, Probleme mit Java-Versionen und nicht mehr funktionierenden alten Arbeitsblättern zu beheben. Es ist das Ziel der GeoGebra-Programmierer immer dafür zu sorgen, dass ein einmal funktionierende Zeichnung auch weiterhin funktioniert. Was bei alten HTML-Exporten irgendwann einmal nicht mehr möglich ist, weil die Java-Version nicht mehr mit den alten Java-Paketen zusammenarbeiten kann. Außerdem wird auf eine Nutzungmöglichkeit auch auf Mobil-Geräten geachtet.

Allerdings wird dafür ein Internet-Zugang benötigt, was von einigen Lehrern bemängelt wird. Das Abspeichern eines Arbeitsblatts und die Weitergabe einer Datei über ein Schulnetz ist natürlich immer noch möglich.

Für diese Abhängigkeit bietet aber GeoGebraTube die Möglichkeit neben einfachen Arbeitsblättern mit Text/Anleitungen davor/dahinter auch erweiterte Seiten zu erstellen und weitere Medien recht bequem einzubinden, auch mehrere Zeichnungen auf einer Seite oder Videos oder interaktive Quizze wie von LearningApps.org.

Eine Strukturierung und Organisation für sich selber oder aber auch für Schüler bieten die GeoGebraBooks, die Sammlungen von Arbeitsblättern sind, wobei man auch als zusätzliche Einteilung Kapitel erstellen kann. Das Design ist auch für kleinere Mobil-Geräte geeignet, denn die GeoGebra-Zeichnungen passen sich an die Größe an. Und wer eine Arbeitsblatt nicht veröffentlichen will, kann es "privat" erstellen oder nur mit Link erreichbar machen.

Praktisch ist die Möglichkeit, die Arbeitsblätter von Kollegen für sich zu kopieren, zu übersetzen oder abzuändern.

Gerade erst frisch ist die Einrichtung von Gruppen ermöglicht worden, die eine Zusammenarbeit von mehreren Kollegen oder Schülern erlaubt.

Überblick - Das CAS im Rahmen der Möglichkeiten von GeoGebra

Mit dem Prezi möchte ich auf einige, üblicherweise nicht allen bekannten Funktionen und Möglichkeiten in GeoGebra eingehen. Außerdem wird das CAS als eine von vielen Ansichten vorgestellt und wie man diese kombinieren kann. Die im Prezi vorkommenden Arbeitsblätter sind im oben erwähnten GeoGebraBook auf GeoGebraTube einsehbar.

Eine kleine Einführung in das GeoGebra-CAS

Unterschied zwischen CAS-Eingabezeile und "normaler" Eingabezeile?

• Eingabe wird in normaler Eingabezeile entsprechend der Programmierung in GeoGebra verarbeitet.
• In der CAS-Zeile wird der Befehl (evtl. nach Bearbeitung und Anpassung) an das CAS-System übergeben und auch die Ausgaben werden nach Bedarf angepasst. Aktuelles System - nach einige Wechseln - ist Giac.

Umgang mit Brüchen

In der normalen Eingabezeile kann ⅓ als Bruch eingegeben werden und man erhält dann die Zahl 0,333, je nachdem wie viele Nachkommastellen festgelegt sind. Man kann diesen Wert mit dem Befehl BruchText[1/3] im Grafik-Fenster auch wieder als Bruch anzeigen lassen. Dies funktioniert so zwar, aber bei Ergebnissen von Rechnungen bzw. aus der Zeichnung wird sich ein Wert ⅓ nicht zuverlässig als Bruch darstellen lassen, da in der Zeichnung immer gerundet wird.

Im CAS wird dagegen der Bruch ⅓ richtig interpretiert und auch so behalten. Zu dem Umgang mit Eingaben und zum Beispiel auch Brüchen, hier die drei Varianten, die jeweils mit den drei ersten Werkzeugen im CAS-Fenster durchgeführt werden.

Eingabe	Werkzeug-Nutzung	Erklärung
1/3	Berechne	Statt das Werkzeug zu anzuklicken, einfach die Eingabetaste drücken. Generell werden alle möglichen Vereinfachungen von Termen mit oder ohne Variablen vorgenommen. Berechnungen und Ergebnisse sind genau.
1/3	Numerisch	Führt dazu, dass Zahlen gerundet angegeben werden, also 0.33. Statt Werkzeug-Nutzung einfach Strg + Enter nutzen. Macht vor allem dann Sinn, wenn man bei einer komplizierten Lösung den ungefähren Wert haben will.
2/6	Behalte Eingabe	Führt dazu, dass die Eingabe erhalten bleibt. Statt Werkzeug einfach Alt + Enter nutzen, zum Beispiel auch zur Kontrolle ob eine Eingabe richtig ist.

Arbeitsauftrag Probieren Sie verschiedene Eingaben von Zahlen und Brüchen mit und ohne Variable aus. Vergleichen Sie auch mit der Eingabezeile. Stelle Sie dann interessante Beobachtungen den Kollegen vor.

Weitere einfache Werkzeuge und Befehle

Das GeoGebra-CAS kennt die üblichen Befehle, die man in CAS als Lehrer z.B. gut nutzen kann, um für Aufgaben die passende Zahlen zu finden.

Hier eine Auswahl der entsprechenden Werkzeuge und Befehle:

Eingabe	Werkzeug	Ausgabe	Erklärung
112		<math>{2^{4} \cdot 7}</math>	Faktorisieren: Zahlen werden in ihre Primzahlen zerlegt.
Faktorisiere[x² - 5x + 6]	-	<math>\left(x - 3 \right) \; \left(x - 2 \right)</math>	Das Faktorisieren kann aber auch als Textbefehl genutzt werden und funktioniert auch bei Polynomen. Der normale Befehl funktioniert nur, wenn die Klammern rationale Zahlen enthalten.
IFaktorisiere[x^2 + x - 1]	-	<math>\left(x + \frac{-\sqrt{5} + 1}{2} \right) \; \left(x + \frac{\sqrt{5} + 1}{2} \right)</math>	... funktioniert auch bei irrationalen Zahlen und ...
KFaktorisiere[x^2 + 4]	-	<math> \left(x + 2 \; i \right) \; \left(x - 2 \; i \right)</math>	... mit komplexen Zahlen. Entsprechend für irrationale komplexe Zahlen mit KIFaktorisiere[...]
2^4*7	<math>{2^{4}}</math> markieren, dann	<math>{16 \cdot 7}</math>	Multiplizieren hat meist den gleichen Effekt wie das Drücken der Eingabe-Taste. Kann aber zum Beispiel verwendet werden, um Teile von Ausdrücken auszumultiplizieren. Entsprechender Text-Befehl lautet Multipliziere[...]
Teilerliste[15]	-	<math>{1, 3, 5, 15}</math>	Teilerliste liefert die Liste aller Teiler der Zahl.
GGT[12, 15]	-	<math>3</math>	Liefert für eine beliebigen Anzahl, auch Listen von Zahlen, den ggT. Entsprechend für den kgV[...].
GGT[x^2 + 4 x + 4, x^2 - x - 6]	-	<math>x+2</math>	... beide Befehle funktionieren auch mit Polynomen.
GemeinsamerNenner[3 / (2 x + 1), 3 / (4 x^2 + 4 x + 1)]	-	<math>4 x^2 + 4 x + 1</math>	GemeinsamerNenner findet bei den zwei gegebenen Brüchen den Nenner und dann den kgV. Funktioniert auch mit Brüchen.

Diese Auswahl ist nur ein kleiner Teil von noch viel mehr Befehlen für das CAS. Einen Überblick erhalten Sie auf dieser Seite, wobei wir einige dieser Befehle noch genauer behandeln werden.

Arbeitsauftrag Probieren Sie selber einige der genannten Befehle mit eigenen Zahlen und Ausdrücken aus. Oder Sie probieren andere Befehle aus der Liste. Gibt es für das teilweise Umformungen von Termen Anwendungen? Probieren Sie dies aus und berichten Sie den Kollegen davon!

Zusammenarbeit zwischen einzelnen Zeilen im CAS

Jede Zeile besteht aus Eingabe und der Ausgabe

Zugriff auf die Ausgabe:

• Anklicken fügt den Wert/Ausdruck in die neue Zeile ein. Es besteht kein dynamischer Zusammenhang!
• Entsprechendes gilt für die Leertaste.
• ) führt dazu, dass die letzte Ausgabezeile in Klammern gesetzt wird (braucht man für Äquivalenzumformungen!)
• Rechtsklick ermöglicht die Auswahl eines Ausgabeformates, um eine Formel woanders einzufügen (LaTeX, Writer, Bild).
• Ausgabe wird unterdrückt, wenn man am Ende der Eingabe ein Semikolon einfügt, z. B. a := 5; (so kann man mehrere Befehle hintereinander in einer Zeile schreiben!)

Zugriff auf die Eingabe:

• = fügt die Eingabe der aus der letzten Zeile erneut ein.
• Anklicken ermöglicht eine Bearbeitung des Befehles. Wurde ein Werkzeug verwendet, muss es erneut angewendet werden.

Alle vorher genannten Zugriffe sind nicht dynamisch, d.h. wenn ich eine Zeile vorher verändere, bleibt die Ausgabe so wie sie ist. Passieren kann das, wenn ...

• man die Zeile davor von Hand ändert.
• definierte Objekte (etwa auch über die Eingabezeile) ändert.

Neben den schon vorher genannten Möglichkeiten gibt es folgenden Varianten statisch oder dynamisch auf vorherige Zeilen zuzugreifen:

• Statische Bezüge kopieren die Ausgabe einer anderen Zeile und werden nicht aktualisiert, wenn sich die kopierte Zeile verändert.
  • # fügt die vorherige Ausgabe als Kopie ein.
  • #5 fügt die Ausgabe aus Zeile 5 als Kopie ein.
• Dynamische Bezüge fügen anstelle einer Kopie eine Verknüpfung mit der Ausgabe einer anderen Zeile ein. Eine spätere Änderungen der verwendeten Zeile wird sich daher auch auf die folgende Zeile auswirken
  • $ fügt die vorherige Ausgabe dynamisch ein.
  • $5 fügt die Ausgabe aus Zeile 5 dynamisch ein.

Arbeitsauftrag Probieren Sie Möglichkeiten zum Zugriff auf Ein- und Ausgaben aus. Probieren Sie zum Beispiel Kettenrechnungen aus. Verändern Sie vorangehende Zeilen und die Auswirkung auf die folgenden Zeilen.

Umgang mit Gleichungen

Vorab eine Warnung! Zu vielen Fehlern und unerwartetem Verhalten führt das Vergessen des Malzeichens. Zwar ist GeoGebra recht flexibel und kann mit Ausdrücken wie <math>3x</math> umgehen. Will man aber zwei Variablen bzw. Parameter so hintereinander eingeben, wie etwa <math>ax</math>, so wird dies nicht als Produkt <math>a \cdot x</math> verstanden sondern als eine einzige Variable mit dem Namen <math>ax</math>. Deshalb sollte zur Sicherheit lieber einmal zuviel das Malzeichen "*" verwendet werden!

Eingabe von Gleichungen

• Eingabe von Gleichung mit einfachem =

3x+2=8 ... hier eine einfache lineare Gleichung oder auch mit anderen anderen mathematischen Funktionen.

• Definition von z.B. einer Funktion mit :=

f_t(x)=t*x^2+3*x-t ... Bestimmung einer Funktion mit Parametern. Das ist in der Eingabezeile nicht möglich, ohne das ein Schieberegler bestimmt wird.

• Benennung eines Objektes über name:

s:f(x)=3 ... es wird eine Gleichung mit dem Namen s erstellt: für welche x hat die Funktion f(x) den Wert 3?

Arbeitsauftrag Für diese "Versuche" sollte das CAS-Fenster und das Grafik-Fenster geöffnet sein! Geben Sie <math>f(x) \, := \, x^{2} - 3 \; x + 4</math>   ein. Probieren Sie folgende Eingabe danach aus: f(3) f(x)=4 Geben Sie <math>g \left(x \right) = 3 \; x - 4</math>   ein. Probieren Sie folgende Eingabe danach aus: g(2) g(x)=5

Lösungen von Gleichungen bestimmen lassen

• mit Werkzeug

• mit Befehlen

Löse[] oder Lösungen[] um eine Lösung für eine Gleichung oder ein System von Gleichungen symbolisch über den reellen Zahlen zu finden.

NLöse[] oder NLösungen[] um numerische Lösungen der angegebenen Gleichung(en) für die Variable x zu finden.

KLöse[] für Komplexe Lösungen.

Die Links verweisen auf Seite im GeoGebra-Hilfe-Wiki. Hier gibt es meist ein paar Beispiele mit Erklärungen zu den Befehlen. So zum Beispiel auch, wie man Startwerte für die Nummerische Berechnung einer Lösung einbaut, wenn die Gleichung nicht nur Polynome enthält, wie man die Variable festlegt, für die eine Lösung bestimmt werden soll oder wie man mit Gleichungssystemen mit mehreren Variablen umgeht.

Beispiel für die Anwendung: Nichtlineare Gleichungssystem

Arbeitsauftrag Geben Sie ein paar Gleichungen ein und lassen sie deren Lösungen bestimmen. Probieren Sie die Lösung von den vorher bestimmten Gleichungen mit f(x) und g(x) zu bestimmen. Was passiert? Probieren Sie Gleichungen wie ... <math>3 x^{2} + 9 x - 54 = 0</math> <math>x^{3} - 12 x = -x^{2}</math> <math>5 (x-2)\cdot(x+2) = 5 x^{2} - 10</math> <math>\frac{1}{2} \cdot 4^{x} = 256</math> <math>-x + 1 = x^{2}</math> Definieren Sie zum Beispiel Funktionen und lassen Lösungen von verschiedenen Gleichungen dazu bestimmen. Probieren Sie Gleichungen mit Ableitungen? GeoGebra versteht f'(x) und f''(x), wenn die Funktion f(x) definiert ist.

Werte in Gleichungen einsetzen

• mit dem Werkzeug

• mit dem Befehl

Ersetze[] ... Erklärungen zur Anwendung auf dem Hilfe-Wiki!

Arbeitsauftrag Schaffen Sie es, im CAS die folgenden Aufgaben zu erledigen? Geben Sie eine Funktion f(x) vor, die mehrere Extrempunkte hat. Bestimmen Sie die Stellen mit waagrechter Tangente. Bestimmen Sie die Funktionswerte für diese Stellen. Idee: So konnte man mit verschiedenen Funktionen ausprobieren, ob man eine "einfache" Lösung für Aufgaben bekommt!

Äquivalenzumformungen

Zum Lösen einer Gleichung mit Äquivalenzumformungen kann man folgendermaßen vorgehen:

• (3x+2=8)-2
• (3x=6)/3
• Ergebnis: x=2

Das geht besonders schnell, wenn man in der nächsten Zeile jeweils ein abschließende Klammer ) eingibt, wodurch die Gleichung aus der vorherigen Zeile übernommen und in Klammern gesetzt wird.

Statt der Gleichung selber kann man Zeilennamen verwenden, wie $ oder $3 oder auch den Namen einer Gleichung, wenn man ihr vorher einen Namen gegeben hat, wie etwa mit g1:3x+2=8. Das erspart viel Schreibarbeit!

Arbeitsauftrag Probieren Sie das Umformen von Gleichungen selber aus, um Lösungen zu bestimmen.

Arbeitsauftrag Schauen Sie sich die beiden folgenden Beispiel an, in denen Äquivalenzumformungen genutzt werden. Auflösen von Gleichungen aus der Physik nach einer bestimmten Variable Quadratische Ergänzung zum Lösen einer quadratischen Gleichung. Fallen Ihnen weitere Anwendungen ähnlicher Art ein?

Arbeitsauftrag Schauen Sie sich das Beispiel aus der Sek I an, in dem der Satz von Vieta über die pq-Formel nachvollzogen wird. Hier werden viele der Ihnen vorgestellten Funktionen und Befehle genutzt. Gibt es ähnliche Anwendungen?

Unterrichtsidee: Äquivalenzumformungen untersuchen in Klasse 8

Äquivalenzumformungen werden am Anfang meist eingeführt als einfache Anweisungen, wie man eine Gleichung "umbaut". Dabei macht man sich gerne das Waagenmodell zunutze.

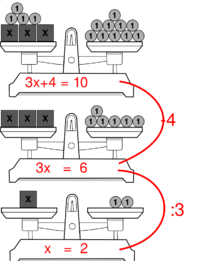
Entsprechend der Idee von Prof. Dr. Regina Bruder (TU Darmstadt) kann man dann erst einmal den Umgang mit Äquivalenzumformungen üben, indem man die Aufgabengrundidee variiert (Erklärungen dazu hier in Tabelle 1 Seite 6/7):

• Äquivalenzumformungen vorgeben und anwenden lassen.
• Äquivalenzumformungen erkennen lassen, wenn zwei Gleichungen vorgegeben sind.
• Vorherige Gleichung bestimmen lassen, wenn die Äquivalenzumformungen und die folgende Gleichung gegeben ist.
• Einfache Gleichungen vorgeben, zu denen man die Lösung mit einer Äquivalenzumformung bestimmen kann.
• Äquivalenzumformungen und die umgeformte Gleichung vorgeben und fragen, ob es richtig durchgeführt wurde

Dann wird für einfache Gleichungen der Art 4x - 6 = 8 ein Verfahren vorgegeben, das man einübt. Das kann mit Aufgaben aus dem Buch geschehen oder man nutzt kleine GeoGebra-Apps, die auch am Handy ein Einüben dieses Schemas erlauben.

Kurzlink und QR-Code für's Smartphone: http://goo.gl/GPR09r

Im nächsten Schritt gilt es aber, sich von diesem starren Schema zu lösen und zu lernen, wie man mit beliebigen Gleichungen umgehen kann und welche Äquivalenzumformung wann mehr Sinn macht. Außerdem muss ein Verständnis dafür entwickelt werden, wie sich die Umformungen auf die Gleichungen auswirken, wie etwa die typischen Fehler beim Teilen vermieden werden.

Dazu könnte das GeoGebra-CAS verwendet werden! Meine Ideen zur Vorgehensweise dazu sind die folgenden:

• Einführung in die Nutzung des CAS (Rechnungen, Lösungen von Gleichungen bestimmen lassen, Lösungen kontrollieren durch Ersetzen von Werten)
• Term-Umformungen üben um x zu isolieren
• Vorgebene Äquivalenzumformungen im CAS anwenden und erkennen, woher das Ergebnis kommt.

Hintergedanken:

• Das GeoGebra-CAS soll bei den Schülern als Hilfsmittel zur Kontrolle ihrer Aufgaben vorgestellt werden.
• Statt nur Schematas vorzugeben, sollen die Schüler Äquivalenzumformungen ausprobieren können, auch wenn sie nicht so sinnvoll sind. Das CAS zeigt das richtige Ergebnis, die Schüler sollen dann verstehen, warum es so herauskommt.

Arbeitsauftrag Gehen Sie das Material auf der Unterseite durch und überlegen Sie, wo es Probleme geben kann? Sehen Sie Vorteile bei dieser Vorgehensweise oder haben weitere Ideen?

Tipp: Auf sehr spielerische Art und Weise, die auch schon für Grundschul- und sogar Kindergartenkinder geeignet ist, führt das App DragonBox Algebra 12+ in das Lösen von Gleichungen ein. Hier wird Algebra geübt, ohne das das Kind es merkt. Bei Interesse können Sie das App bei mir ausprobieren. Playstore, iTunes, Produkt-Trailer , Vorstellungs-Video

Zusammenarbeit des CAS mit der Grafik-Ansicht in GeoGebra

Um eine gute Zusammenarbeit zwischen CAS und der Grafik-Ansicht zu ermöglichen, hat man sich von Seiten der Programmierer bemüht, die Anzeige durch das Sichtbarmachen über den kleinen Kreis links neben der Ein-/Ausgabe-Zeile zu erlauben. Auch wenn die Anzeige nicht automatisch erfolgt ist. Dabei wird die Eingabe meist abgeändert, um die notwendigen Eingabe zu erzeugen.

Wie schon erwähnt ist die Grundvoraussetzung, dass ein im CAS definiertes Objekt dargestellt werden kann, dass es als Objekt einen Namen bekommt und definiert ist. Das gilt vor allem für Funktionen. Wenn man deshalb gleich die Objekte bei der Eingabe benennt, kann man auch einen eigenen Namen auswählen.

Außerdem ist noch der Unterschied erwähnenswert, ob man zum Beispiel x^2 ...

• in die Eingabezeile eingibt - es wird eine Funktion <math>f(x)=x^2</math> erzeugt und der Graph im Koordinatensystem der Grafik-Ansicht angezeigt.
• in dem CAS eingibt - es wird als Term übernommen und angezeigt, aber keine Funktionsgraph dargestellt. Es verändert sich nichts, da keine Vereinfachungen vorgenommen werden können. Gleiches gilt für y=x^2.

Die Angabe eines Namens reicht aber auch nicht, wenn man eine Funktion definieren will.

• <math>f:=x^2</math> führt nicht dazu, dass ein Graph angezeigt wird. Die Variable f ist hier durch die Variable x definiert. Die Eingabe f(5) führt zur Ausgabe von <math>x^2</math>. Mit Hilfe von Ersetzen[f,{x=5}] bekomme ich aber einen Wert, nämlich 25.
• <math>f(x):=x^2</math> dagegen erzeugt eine Funktion f, die gleich im Koordinatensystem der Grafik-Ansicht angezeigt wird. Auch f(5) führt dazu, dass man den Funktionswert an der Stelle 5 berechnen bekommt.

In allen vorgenannten Fällen können die eingegebene Objekte sichtbar gemacht werden, durch Klick auf den kleinen Kreis. Es findet aber immer die Anpassung an die notwendige Schreibweise statt!

Umgang mit Gleichungssystemen in der Sek I

Zur Eingabe von Gleichungen für ein Gleichungssystem gibt es mehrere Möglichkeiten:

• Man definiert die Geraden über zwei vorhandene Punkte, was mit dem Befehl Gerade[Punkt1,Punkt2] sowohl im CAS als auch in der Eingabezeile möglich ist. Die Gerade erhält automatisch einen Namen, den man auch bei weiteren Operationen verwenden kann, wie etwas bei Äquivalenzumformungen, Einsetzungen, Gleichsetzen, ...
• Gibt man einen Term ohne Namen an, etwa 3*x-2=5*y, so wird die Gleichung nicht als Gerade angezeigt. Es sind aber alle Operationen möglich, wie Äquivalenzumformungen, Einsetzungen, Gleichsetzen. Allerdings muss man bei der dynamischen Verwendung dieser Gleichung zwingend per $-Symbol referenzieren, da man keinen Namen hat, mit der man die Gleichungen "ansprechen" kann.
• Bekommt die selbe Gleichung einen Namen, wie etwa I:3*x-2=5*y, so wird die Gerade im Koordinatensystem angezeigt.

HINWEIS: Klammern und einige andere Symbole können nicht für Namen verwendet werden!

Gleichungssystem lösen lassen

Nehmen wir an, wir haben zwei Geraden g1 und g2 definiert. Mit Löse[{g1,g2}] wird die Lösung für x und y angezeigt.

Die doppelte geschweifte Klammern bei der Lösung kommen daher, dass es bei anderen Gleichungen ja zu mehreren Lösungen kommen kann. Ein solche Lösung könnte dann so aussehen {{x=1,y=-3},{x=-5,y=2}}

• Der Befehl Schneide[] kann zuverlässig nur bei Funktionen verwendet werden. Die Anwendung des Löse[]-Befehls um bei Funktionen den Schnittpunkt zu finden ist etwas umständlicher. Er müsste Löse[{y=f(x),y=g(x)}] lauten.

Arbeitsauftrag Probieren Sie den Löse[]-Befehl für eigene Gleichungen und Funktionen aus. Wie ist die Lösung bei parallelen Geraden? Wie bei identischen Geraden?

Lösungsverfahren nachvollziehen

Einsetzungs-, Gleichsetzung,- und Substitutionsverfahren können im CAS mit Hilfe der Äquivalenzumformungen der Gleichungen nachvollzogen werden. Zusätzlich benötigt man dann aber noch den Befehl RechteSeite[] bzw. LinkeSeite[], um auf Teile einer Gleichung zugreifen zu können, um diese zum Beispiel für eine Variable einzusetzen.

Arbeitsauftrag Wenden Sie bei den gegebenen Geraden das Einsetzungverfahren an. Legen Sie die Geraden g1:3x+4=2y und g2:4x-2y=1 an. Nutzen Sie zum Einsetzen den folgenden Befehl: Ersetze[g2, 2y,LinkeSeite[g1]] Bestimmen Sie die Lösung für die übrigbleibende Gleichung (mit Löse[] oder per Äquivalenzumformung)

Arbeitsauftrag Überlegen Sie sich, wie Sie das Gleichsetzungsverfahren bei den Gleichungen g1:3x-2=2y und g2:-3x=1+4y anwenden können. (Lösungsvorschlag) TIPPs: Wenn Sie eine Gleichung umformen, können Sie ihr einen neuen Namen geben, z.B. g1'. Es können in einem Schritt auch mehrere Äquivalenzumformungen durchgeführt werden.

Arbeitsauftrag Führen Sie mit den Gleichungen g1:3x-2y=-1 und g2:-x-4y=5 das Additionsverfahren durch. (Lösungsvorschlag) TIPPs: Verwenden Sie wieder einen neuen Namen für umgeformte Gleichungen. Die Addition der angepassten Gleichungen kann man einfach mit den Namen der Gleichungen durchführen, es ist also zum Beispiel g1+g2 möglich.

Lösungen anzeigen lassen

Wenn man nun schon die Lösungen von Gleichungssystem bestimmt hat, dann möchte man diese Lösungen vielleicht auch anzeigen lassen. Dazu kann man den Kreis links an der Zeile nutzen, aber es funktioniert nicht immer.

Wenn man die Lösung eines 2x2 Gleichungssystems gefunden hat, so kann die Anzeige des Schnittpunktes funktionieren, aber nur dann, wenn x- und y- in der richtigen Reihenfolge in der Lösung erscheinen. Wird zuerst y angegeben, so werden statt eines Punktes zwei passende Geraden ausgegeben. Dies kann man korrigieren. indem man beim Löse[]-Befehl die Reihenfolge der auszugebenden Variablen richtig festlegt.

Alternativ kann man auch aus den Lösungen einen Punkt zusammensetzen, aber das ist nicht so einfach.

Hier der Screenshot eines Beispiels (bei dem die Anzeige des allerdings auch automatisch funktionieren würde!)

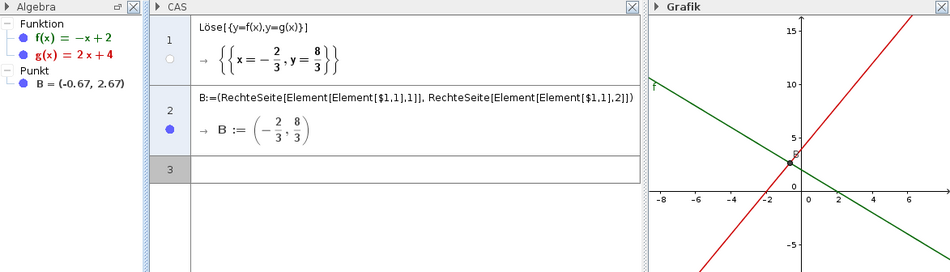
Nehmen wir diesen Befehl B:=(RechteSeite[Element[Element[$1,1], 1]],RechteSeite[Element[Element[$1,1], 2]]) mal auseinander:

• mit B:= lasse ich mir das Ergebnis anzeigen. Das Ergebnis ist natürlich ein Punkt und der wird in runden Klammer angegeben, wobei die Koordinaten durch Komma getrennt sind.
• mit dem Befehl Element[Liste, Position] greife ich auch Elemente in einer Liste zu. Mit Element[$1,1] betrachte dabei die Liste aus Zeile 1 ($1) und zwar das erste Element davon. Die Ausgabe in der Zeile 1 ist eine Liste, weil außen geschweifte Klammern stehen. Allerdings habe ich nur ein Element da drinnen, nämlich die geschweifte Klammer mit den Lösungen, also hier {x=-2/3,y=8/3}.
• Da {x=-2/3,y=8/3} ja wieder eine Liste ist muss ich, um auf x=-2/3 zugreifen zu können, erneut den Befehl Element[Liste, Position] anwenden. Mit Element[Element[$1,1], 1] erhalte ich als Ergebnis x=-2/3.
• Um auf y=8/3 zugreifen zu können, nutze ich den Befehl Element[Element[$1,1], 2] und greife damit auf das zweite Element der Liste {x=-2/3,y=8/3} zu.
• Da ich von x=-2/3 nur die rechte Seite brauche nutze ich den Befehl RechteSeite[Element[Element[$1,1], 1]] und damit habe ich den x-Wert. Gleiches mache ich für den y-Wert des Schnittpunktes über RechteSeite[Element[Element[$1,1], 2]].

Angesicht dieses Befehls-Monstrums ist die Frage, ob ich diesen Weg wirklich gehen will, oder dann doch einfach über die Eingabezeile die eventuell gerundeteten Koordinaten der Schnittpunkte anzeigen lasse. Die genauen Werte kann ich ja immer noch im CAS ablesen, bzw. mir dazu gerundete Werte anzeigen lassen. Einfache Werte, wie hier im Beispiel die Brüche, lassen sich zwar leicht (von Hand) eingeben, allerdings ist dann diese Verknüpfung nicht mehr dynamisch.

Beispiele aus der Analysis

Kurvendiskussion

Letztendlich ist die Kurvendiskussion nichts anderes als die Bestimmung diverser Eigenschaften einer Funktion, wobei es teilweise spezielle Befehle gibt, die man einfach nur anwenden muss. Hilfreich sind natürlich auch die Befehle zum Lösen von Gleichungen, die Sie schon kennengelernt haben. Ein konkretes Beispiel:

• Angabe der Funktion f(x):=x*(1-ln(x)), wodurch diese auch gleich gezeichnet wird.
• Mit Löse[f(x)=0] bestimmt man die Nullstellen der Funktion bzw. mit Löse[f'(x)=0] die x-Werte bei denen man eine waagrechte Tangente hat.
• Der Befehl Grenzwert[f,∞] sollte klar sein, wobei man das Symbol ∞ mit Hilfe der Sonderzeichenauswahl in der Texteingabezeile auswählen und eingeben kann (Symbol α).

Arbeitsauftrag Probieren sei selber eine Kurvendiskussion mit der vorgeschlagenen Funktion oder einer eigenen. Wie könnte man Funktionswerte bestimmen (von Extremstellen, ...)? Oder die Werte der zweiten Ableitung zu den Extremstellen?

Extremwertaufgaben

Die Behandlung von Extremwertaufgaben in GeoGebra hat den Vorteil, dass man hier auch grafische Darstellungen einbinden kann. Außerdem kann per Spur die zu untersuchende Funktionen betrachtet werden und man kann den ungefähren Wert des Extremums ablesen. Im CAS kommt man mit den schon erlernten Befehlen aus.

Der österreichische Kollege und langjährige Mitarbeiter im GeoGebra-Team Andreas Lindner hat zu diesem Bereich einige Aufgaben umgesetzt, bei denen auch immer die Grafik-Ansicht eingesetzt wurde. Sie sind im GeoGebra-Book eingefügt.

• Minimaler Flächeninhalt eines Parallelogramms

Zeichnerische Aufgabe, bei der in der ersten Grafik-Ansicht die Aufgabe zu sehen und auszuprobieren ist. In der zweiten Grafik-Ansicht wird die Funktion als Spur eingezeichnet.

• Balken mit maximaler Querschnittsfläche

In einer Grafik-Ansicht verschönert ein Bild als Hintergrund die Darstellung. Die zweite Grafik-Ansicht enthält wieder einen Punkt von dem die Spur eingezeichnet wird. Die Funktion ist dünn eingezeichnet. Eine Tangente erleichtert das Finden des Maximums.

• Saftbox

Bei Volumen-Aufgaben kann natürlich auch die 3D-Ansicht genutzt werden, so dass nicht nur das Netz in 2D sondern auch der Körper in 3D betrachtet wird.

• Kegel mit eingeschriebenem Zylinder

In diesem Beispiel wird im CAS auch die Möglichkeit zum Umformen von Gleichungen genutzt, um den zu maximierenden Term zu bestimmen.

• ... und weitere Beispiele in einem der GeoGebraBook-Kapitel.

Nutzung von Parametern

Bereits in der Grafik-Ansicht konnte man in GeoGebra mit Parametern arbeiten und diese über die Eingabezeile festlegen. Dazu verwendet man Schieberegler (eine definierte Variable, die sichtbar gemacht wird). Allerdings hat man so natürlich immer nur die Funktion für einen Parameter, die man anzeigen kann. Mit Hilfe von Spuren kann man dann z.B. Ortskurven sichtbar machen. Oder man nutzt den Befehl Ortslinie[].

Gib man im CAS eine Funktion mit Parameter an, so hängt die Darstellung davon ab, ob der Parameter definiert ist oder nicht:

• Ist der Parameter festgelegt, ob als Schieberegler oder über das CAS bzw. die Eingabezeile festgelegt, so wird nach der Eingabe automatisch der Parameter in der Gleichung gleich durch den Parameterwert ersetzt.

Beispiel: Schieberegler a wurde angelegt und f_a(x):=x^2-3*a*x eingegeben.

• Definiert man eine Funktion in Abhängigkeit von x und dem Parameter a wird die Gleichung belassen.

Beispiel: Schieberegler a wurde angelegt und f(a,x):=x^2-3*a*x eingegeben.

• Existiert kein Schieberegler zu einem gegebenen Parameter, so bleibt der Funktionsterm wie angegeben. Allerdings kann die Funktion auch nachträglich nicht mehr mit einem nachträglich erstellten Schieberegler verknüpft werden, wie das im ersten Beispiel der Fall war.

Arbeitsauftrag Die Lösung für das Parameter-Problem: Legen Sie die Funktion f(a,x):=x^2-3*a*x an. Erstellen Sie einen Schieberegler a in der Grafik-Ansicht. Definieren Sie eine neue Funktion f_a(x):=f(a,x) Erklärung: In der letzten Zeile wird die Variable a verwendet, die ja nun definiert ist. Deshalb kann man die Parameter-Funktion für einen bestimmten Parameter-Wert zeichnen lassen. ACHTUNG: Sinnvoller ist es vermutlich, wenn man einen Schieberegler mit anderem Namen definiert. Denn auch bei nachträglichen Änderungen einer Eingabe kann es dazu kommen, dass in Zeilen die auf diese Änderung folgen, dann doch noch der inzwischen definierte Parameter eingesetzt wird. Um das zu umgehen kann man hier zum Beispiel einen Schieberegler b erstellen und f_a(x):=f(b,x) eingeben, um die zum Schieberegler gehörige Parameterfunktion anzuzeigen. Lösungsbeispiel zur Bestimmung der Ortskurve des Extremums bei der oben angegebenen Funktion.

Steckbrief-Aufgaben

Eine weitere Anwendung von Parameter ist die Bestimmung von Funktionen aufgrund von vorgegebenen Eigenschaften. Solche Steckbriefaufgaben lassen sich ebenfalls im GeoGebra-CAS umsetzen.

Beispiele, die von Andreas Lindner erstellt wurden:

Beispiel 1 und Beispiel 2

Hinweise: In den Eingabezeilen wurden teilweise die Eingabe nur übernommen und nicht ausgewertet (✓). Deshalb wird auch nicht die Ableitung bestimmt und dann in der Ausgabe angezeigt, wenn man f'(x) verwendet.

Beispiele aus der Linearen Algebra

Die 3D-Ansicht bietet schon viele Möglichkeiten für den Einsatz im Unterricht in der Oberstufe für Lineare Algebra/Analytische Geometrie. Leider fehlen noch einige Funktionen, wie die Definition von Ebenen in allen Varianten.

Die meisten Lösungsverfahren lassen sich zeichnerisch durchführen, was gerade für Grundkurs-Schüler sehr bequem ist. Allerdings bekommt man dann nur gerundete Werte als Lösungen. Gerade, um ein Verfahren anschaulich für schwache Schüler dazustellen, ist das schon ausreichend. Ebenso für die Überprüfung einer eigenen Rechnung, allerdings wird dabei natürlich noch nicht klar, wie man die Zwischenschritte praktisch durchführt.

Zusammen mit dem CAS kann man nun Berechnungen exakt vornehmen und diese auch in der Ansicht darstellen lassen. Hier einige Beispiele, die kommentiert werden.

Bedanken möchte ich mich in dem Zusammenhang bei dem GeoGebraTube-Benutzer hawe, der für mich eine umfassende Vorarbeit geleistet hat und ausgetüftelt hat, wie man das in GeoGebra anwenden kann.

Beispiel-Datei: Lot auf Gerade im R3

Schritt	Was ?	Wie?
1	Q:=(1,-2,1)	Zuerst wird der Punkt bestimmt, von dem aus der Abstand bestimmt werden soll. Das kann auch in der Eingabezeile geschehen, wobei dann bei der Eingabe den Doppelpunkt weglassen kann, also Q=(1,-2,1). Der Punkt wird gleich in der 3D-Ansicht angezeigt.
2	g(t):=(1,0,2)+t*(-1,2,2)	Hier erfolgt die Eingabe der Gerade zu der der Abstand bestimmt werden soll. Auch hier kann die Eingabe über die Eingabezeile geschehen, wenn man den Doppelpunkt weglässt, also g(t)=(1,0,2)+t*(-1,2,2). Als Ergebnis wird ein Vektor ausgegeben, der t innendrin enthält. Für Schüler ist das natürlich ein wenig ungewohnt.
3	A:=g(1)-g(0)	Es erfolgt hier die Berechnung des Normalenvektors für die Hilfsebene. Allerdings wird hier ein Punkt erzeugt, der in der normalen 3D-Ansicht nicht zu sehen ist, weil er außerhalb des sichtbaren Bereiches liegt. GeoGebra ist da übrigens nicht so kritisch, was die Unterscheidung zwischen Punkten und Vektoren betrifft. Es folgt dabei einer Idee des österreichischen Didaktikers Günther Malle (Artikel dazu). So können Punkte und Vektoren gleich verwendet werden.
4	E1(x,y,z):=(g(1)-g(0))*((x,y,z)-Q)	Hier folgt die Festlegung der Hilfsebene, die senkrecht zur Gerade g liegt und den Punkt Q auf der Geraden enthält. Allerdings wird diese Ebene noch nicht angezeigt sondern ist eine Funktion mit drei Variablen x,y,z. Man benötigt sie für die Berechnungen im CAS, da die Nutzung von Ebenengleichungen im 3D für Berechnungen noch nicht in GeoGebra eingebaut sind. Aber vermutlich wird das auch noch kommen.
5	E_1:=E1(x,y,z)=0	Hier wird eine sichtbare Ebene erzeugt, indem man den Term der Funktion für eine Koordinatengleichung verwendet.
6	x(g(t))	Die Bestimmung des Schnittpunktes erfolgt durch Einsetzen der Geradengleichung in die Ebenengleichung. Dazu kann man durch eine solche Eingabe die x-Koordinate der Gerade bestimmen, also quasi die erste Zeile.
7	E1(x(g(t)),y(g(t)),z(g(t)))	Um den Parameterwert für den Schnittpunkt zu bestimmen, nutzt man das vorher vorgestellte Prinzip bei allen drei Koordinaten und setzt jeweils die Koordinaten der Geraden in die vorher definierte Funktion E1(x,y,z) ein.
8	Löse[E1(x(g(t)),y(g(t)),z(g(t))),t]	Allerdings liefert die vorherige Zeile noch keinen Wert für den Parameter. Dazu braucht man den Befehl Löse[], wobei eigentlich keine Gleichung sondern nur ein Term angegeben ist. Tatsächlich wird die Eingabe so behandelt, als ob man eingibt: Löse[E1(x(g(t)),y(g(t)),z(g(t)))=0,t].
9	F:=Ersetze(g(t),Löse(E1(x(g(t)),y(g(t)),z(g(t))),t))	Hier wird nun endlich der Schnittpunkt der Hilfsebenen mit der Geraden bestimmt, indem man die Lösung für t in die Geradengleichung g(t) mit dem Befehl Ersetze[] einsetzt. F ist dann der Lotfußpunkt von Q auf die Gerade g. Im Grunde genommen hätte man die Schritte 6 - 8 weglassen können. Sie dienten nur der Erläuterung dieser recht verschachtelten Zeile.
10	Vektor[Q,F]	Das ist der Lotvektor von Q auf den Lotfußpunkt F. Allerdings wird er, wenn man ihn so berechnet als Vektor vom Ursprung aus eingezeichnet. ...
11	Lotvektor:=Verschiebe[Vektor[Q,F],Q]	So, oder auch mit einer anderen Möglichkeit, kann man den Vektor an der Stelle anzeigen lassen, wo er erwartet wird. Als Name wird dann "Lotvektor" angezeigt.
12	d:=sqrt(Lotvektor^2)	Und hier nun endlich die Länge des Lotvektors und damit der Abstand von Q auf die Gerade g. Übrigens bräuchte man den verschobenen Lotvektor nicht. Man könnte für die Berechnung auch Vektor[Q,F] verwenden.

Beispiel-Datei: Schnittgerade bei Ebenen in Koordinatenform bestimmen

Hinweis: Die Referenzen wie $7 und $9 beziehen sich auf die Zeilen, wie sie in dieser Beispiel-Datei verwendet wurden.

Schritt	Was ?	Wie?
1	E1(x,y,z):=2x+2y-z-6	Es wird eine Funktion mit drei Variablen festgelegt/definiert für die erste Ebene. Dies ist notwendig, um mit der Funktion im CAS arbeiten zu können. ...
2	E2(x,y,z):=6x+9y+2z+22	... Ebenso für die zweite Ebene. Allerdings kann man diese Funktion nicht darstellen.
3	E_1:=E1(x,y,z)=0 und E_2:=E1(x,y,z)=0	Hier wird die Ebene festgelegt und kann dann auch sichtbar gemacht werden. Man beachte den Unterschied bei der Namensgebung: E1 ist der Name der Funktion für das CAS und E_1 (also mit tiefgestellter 1!) ist der Name für die Ebene, die man in Koordinatendarstellung angibt.
4	{E1(x,y,t)=0,E2(x,y,t)=0}	Man erstellt eine Liste, die die Ebenen enthält, bei denen nun aber die Variable z durch einen Parameter t ersetzt wird. Das macht man, weil t der Parameter für die Schnittgerade werden soll.
5	Löse[$7,{x,y}]	Es werden die Lösungen für die Variablen x und y bestimmt und dies in Abhängigkeit von der Variable t, was automatisch geschieht. Dabei bezieht man sich auf die Zeile 7, was natürlich angepasst werden muss, wenn es eine andere Zeilennummer ist.
6	g(t):=Ersetze[(x,y,t),$9]	Damit die Gerade dargestellt werden kann, muss man diese mit Hilfe der vorher bestimmten Lösungen festlegen. Dazu wird ein allgemeiner Vektor genommen, bei dem z = t ist und x und y werden durch die Vorherigen Lösungen ersetzt. Den Richtungsvektor kann man so nicht direkt erkennen, aber herausarbeiten.

Beispiel-Datei: Abstand zweier windschiefer Geraden (über die Hesse'sche Normalenform)

Schritt	Was ?	Wie?
1	g_1(t):=(4,5,3)+t*(1,2,1)	Hier wird die erste Gerade g_1 (1 tiefgestellt) in Parameterform festgelegt. Diese kann gleich angezeigt werden. Der Parameter ist hier t, es kann aber auch ein anderer verwendet werden z.B. λ.
2	g_2(l):=(1,-2,2)+l*(-1,2,0)	Nun die zweite Gerade. Diese Geraden sollte man auch über die Eingabezeile festlegen können, allerdings kann man dann auf die Verwendung des Doppelpunkts bei der Definition verzichten, also nur g_2(l)=(1,-2,2)+l*(-1,2,0)
3	r_1:=g_1(1)-g_1(0) und r_2:=g_2(1)-g_2(0)	Man bestimmt für die beiden Geraden die Richtungsvektoren, indem man sich jeweils zwei Punkte auf den Geraden gestimmt und deren Differenz berechnet g(1)-g(0).
4	O_1:=g_1(0)	Hier wird ein Ortsvektor erstellt, den man für die Festlegung einer Hilfsebenen braucht.
5	n:=Kreuzprodukt[r_1,r_2]	CAS-Eingabe	Für die Ebene wird der Normalenvektor bestimmt ...
6	<n_1:=1/sqrt(n^2)*n/code>	... und dieser normiert auf die Länge 1.
7	E1(x,y,z):=n_1*((x,y,z)-O_1)	Wie im vorherigen Beispiel wird die Gerade in Hesse'schen Normalform als Funktion mit drei Variablen festgelegt aber so noch nicht angezeigt. Braucht man für weitere Berechnungen!
8	E_1:=E1(x,y,z)=0	So wird die Ebene wieder sichtbar gemacht, indem eine Eben definiert wird. Wichtig ist der andere Name dieser Ebene, also hier E_1 statt E1 für die Funktion.
9	O_2:=g_2(0)	Ich brauche einen Punkt auf der zweiten Geraden, um diesen in der Hesse'schen Normalform einzusetzen, um den Abstand erhalten zu können.
10	d:=n_1*(O_2-O_1)	Aufgrund des normierten Normalenvektors bekomme ich so den Abstand der zwei windschiefen Geraden.

Technische Infos zu meinem Unterricht und GeoGebra

• Screencast können mit verschiedenen Programmen aufgenommen werden.

• Ich habe (hatte) seit zwei Jahren Screecast-o-matic genutzt, weil es in Java programmiert ist und unter Linux lief. In der neuen Version läuft es leider nicht mehr unter Linux.

Vorteil: Quasi ohne Installation zu nutzen, einfach in der Bedienung, kostenlos bis 15 Minuten je Aufnahme mit kleinem Wasserzeichen in der Ecke, direkter Upload zu YouTube möglich.

• Bei Windows-Benutzern ist auch Camstasia beliebt. Habe es aber nicht benutzt!

• Die Lösungen für meine Schüler veröffentliche in einem öffentlichen Evernote-Verzeichnis. Der Grund dafür ist vor allem, dass ich auf meinem Galaxy Note mit der App Lecture Notes ein perfektes Schreibprogramm habe (markieren, korrigieren, verschieben, drehen, spiegeln, ...) und dies dann direkt in Evernote veröffentlichen kann.

• Eine Liste aller Tastenbefehle sind im Hilfe-Wiki zu finden.