AK GeoGebra - Terme und Gleichungen

Sammlung von Ideen zum Thema - mit und ohne GeoGebra

Arbeitsgruppen am 31.05.2016, 10:00 bis 17:00 Uhr

• Instituts-GeoGebra-Book zur Sammlung von Applets
• MindMap
• /Klasse 7 - Ideensammlung Rationale Zahlen/

GeoGebra zur Einführung in Grundvorstellungen zu Terme

Mitglieder: Ralf (ab 14:00 Uhr), Dirk, Birgit

Material:

• 1 Probleme beim Arbeiten mit Probleme beim Arbeiten mit Variablen, Termen und Variablen, Termen und Gleichungen Gleichungen
• Terme, Gleichungen und Formeln in Klasse 7 bis 9

GeoGebra zum Üben von Termen, ...

• Katalin (ab 14:00 Uhr), Isabel, Thomas

Anwendungen

• Martin (ab 14:00 Uhr), Georg, Jochen

Vorhandene Ideen und Materialien

Einführung von Variablen in Termen (Ende Klasse 7)

Terme selber aufstellen bzw. benutzen

• Mathematik für Minecraft-Bauer ... das Thema kommt vor allem bei Schülern gut an, die selber Minecraft spielen. Die Idee kam mir selber beim Bauen. Siehe ARBEITSBLATT und ein Video (4:30 Min.), indem ich es in Minecraft direkt zeige.

• Beispiel aus Buch Elemente der Mathematik 7 (Schroedel) Abgrenzen eines Beetes mit vorgegebenem Zaun: Mit 6 m Zaun sollen ein Beet in einer Hausecke abgegrenzt werden. Term x*(6-x) als eine Verallgemeinerung für verschiedene Varianten. Hier kann schon klargemacht werden, dass nicht jede Zahl Sinn macht, es gibt für Terme zu Sachthemen meist Definitionsbereiche. Außerdem wird die Schreibweise A(x) geklärt.

• Vergleich zweier Telefontarife: Entweder selber aufstellen der Terme oder diese vorgeben z.B. A(x) = 10+0.1*x und B(x)=0.2*x, wobei x für Minuten steht.

Die Schüler sollen lernen, wie man die Variable x nutzt und Zahlen einsetzt. Auch hier kann man diskutieren, wie der Definitionsbereich ist. Dabei stellen die Schüler unterschiedliche Vermutungen/Begründungen an. Einige argumentieren das negative Zahlen nicht sein können, da man nicht -5 Minuten telefonieren kann. Einige stören sich auch an 0 Minuten (Zitat: "Wer leistet sich eine Flat, wenn er nicht telefoniert"). Andere schauen nach dem Ergebnis ob das Sinn macht. So sind negative Werte als Ergebnis des Terms wie z.B. bei B(-5) nicht sinnvoll, weil man da ja Geld bekommen müsste. Bei A(-5) ist das aber nicht der Fall.

Ein eine gemeinsame Tabelle eingetragen müssen die Schüler den Unterschied zwischen der Spalte/Zeile verstehen, die Werte für x festlegt und den Spalten in denen man etwas berechnet. Dabei ist x nicht als ein Term zu verstehen! Und es sollte noch einmal zurückblickend erinnert werden, dass man zwei Zuordnungen hat, nämlich x->A(x) und x->B(x)

Das Eintragen von Wertepaare, wie bei den Zuordnungen gelernt, kann den Schülern verdeutlichen, dass man so z.B. die Lage der Graphen zeigt, welcher Tarif billiger ist. Und man kann erkennen bzw. zeichnerisch bestimmen (Linienverlängern), ab wann sich ein Tarif lohnt. Statt zu probieren kann man den Wert zeichnerisch bestimmen.

• Maximales Volumen einer Box: Ein Quadrat mit einer Seitenlänge von 20 cm zu einer Box umgebaut werden. Dazu werden in allen vier Ecken kleine Quadrate ausgeschnitten.

Nachdem anhand einer Skizze erklärt wurde, wie die Box gebaut werden soll, wird im Plenum nach mögliche Werte für die Größe der kleinen Quadrate gefragt. Die Schüler machen Vorschläge und werden nach den zu erwartenden Seitenlängen gefragt.

Wer einen Wert genannt hat, bekommen den Auftrag die entsprechende Box selber zu bauen. So stellt man sicher, dass verschiedene Boxen gebaut werden. Lehrer stellt "Tesa" zur Verfügung. Jeder soll außerdem das Volumen seiner Box berechnen. Dies ist nicht schwer, da man die Seitenlängen ja messen kann.

Die Schüler erkennen hier von alleine, das die Seitenlänge der kleinen Quadrate (ich nenne es mal x) nicht größer als 10 sein dürfen.

An der Tafel werden alle Wertepaare gesammelt, wobei auch gezeigt wird, wie berechnet wurde. Man kann erahnen, wo etwa das Volumen am größten ist. Allerdings muss klar sein, dass wir nicht alle Werte für x ausprobiert haben und es könnte Werte geben, die zwischen unseren ausprobierten liegen.

Die Berechnung wird noch mal gesichert, indem man die Berechnung für ein beliebiges x aufschreibt. V(x)=x*(20-2x)²

In GeoGebra eingeben ergibt der Term V(x) eine Kurve, bei der man schließlich erkennen kann, bei welchem x man (etwa) das maximale Volumen bekommt. Dabei sollte man noch einmal klären, was die Koordinaten eines Punktes bedeuten, warum der höchste Punkt das größte Volumen darstellt und wie man den dazugehörigen x-Wert findet.

Zur Unterstützung habe ich einige GeoGebra-Zeichnungen erstellt, siehe verlinktes Kapitel im GeoGebra-Buch: http://tube.geogebra.org/book/title/id/79636#chapter/153

• Punktmuster aus Elemente der Mathematik 7 (Schroedel) Ein recht abstraktes Thema, da es nicht wirklich Anwendungsbezogen ist. Allerdings habe ich die Erfahrung gemacht, dass man durch bewussten Aufschreiben und farbiges Markieren der einzelnen Bestandteile es verständlich machen kann.

Mit drei Farben wird markiert:

• Welche Punkte treten überall einmal auf.
• Welches sind die sich veränderlichen Punkte und welche Punktepäckchen treten dabei immer wieder auf.
• Wo taucht die Nummer des Musters im Muster selber auf.

Die Anzahl der Punkte bei den ersten Mustern werden nicht einfach als Ergebnis aufgeschrieben sondern systematisch gezählt. Beim Aufschreiben dieser Rechung tauchen wieder die gleichen Farben auf, wie schon vorher, damit man sie zuordnen kann.

Dieses Prinzip können die Schüler dann bei weiteren Beispiel selber anwenden und haben so eine klare Anleitung wie sie vorzugehen haben.

Hier der Eintrag eine Schülern in das Lerntagebuch zu den Punktmustern. Es war als Hausaufgabe auf, an einem selber gewählten Beispiel zu erklären, wie man auf die Formel für die Punkte kommt.

<popup name="Hefteinträge einer Schülern">

</popup>

FOLIE, mit der die Lösungen für verschiedene Punktmuster besprochen werden.

• 
  x-beliebig ... Zahlen bei Würfelgebäuden aus Mathebu.ch (schweizer Schulbuch, dass inzwischen auch in D verfügbar ist)

Hier bekommen die Schüler von mir eine Tüte mit kleinen 1cm³ Holzwürfelchen, die ich mal im 1000er Pack gekauft habe. Für 8 Gruppen habe ich Würfelchen in einer kleinen Plastik-Tüte zusammengefasst. Das Ganze ist recht kompakt transportierbar. Dazu die Anweisungen laminiert, es gibt aber auch kleinere Zettel, die die Schüler zum Zeichnen nutzen sollen. Siehe GESAMMELTES MATERIAL

Die Arbeitsblätter werden dann möglichst in 4er (oder 3er) -Gruppen bearbeitet, die ich selber so zusammenstelle, dass immer mindestens ein sehr guter Schüler dabei ist.

Die meisten Aufgaben können von den Schülern gut bearbeitet werden, wenn sie bei den Punktmustern gelernt haben, wie man die gesuchten Anzahl systematisch bestimmt.

Ein weitere Idee, die nicht so leicht umzusetzen ist, wäre das Bauen der Würfel in Minecraft. Hier kann man leicht mit farbigen Klötzchen die Muster strukturieren. Dies habe ich in einem Video erklärt.

Die Bilder der Würfel habe ich übrigens in Inkscape erstellt. Dazu habe ein ich isometrisches Gitter verwendet. In einem Video VIDEO erkläre ich, wie ich in Inkscape das isometrische Gitter erstelle und wir dann die Würfel erstellt habe. Eine umfangreichere Sammlung von Anleitungen zum Einstieg in Inkscape gibt es hier.

Termumformungen, Rechenregeln Formeln

Teil eigene Zeichnungen teils Fundstücke von anderen in GeoGebra:

einige Materialien müssen wegen der Umstellung auf HTML5 überarbeitet werden.

• Veranschaulichung des Assoziativ-Gesetzes
• Veranschaulichung des Distributiv-Gesetzes
• 1. Binomische Formel (mit Zahlen oder Variablen)
• Herleitung 2. Binomische Formel
• Herleitung 3. Binomische Formel
• Binomische Formel "hoch drei"
• Terme mit Legosteinen veranschaulichen (dieses und die weiteren Zeichnungen im GGB)

Wiskunde-Java-Applets aus den Niederlanden: Das ist hier nur eine Auswahl, wo man Terme durch Flächen repräsentiert bekommt und umgekehrt. Allerdings kann man das selber ändern und anpassen.

Bis auf das erste sind bei mir keine von denen leider gelaufen. Was sicher auch an der Java-Version unter Linux liegt.

• Geometric Algebra 2D ... zum selber herumspielen und eigenen Aufgaben
• Geometric Algebra 2D Problems 1
• Geometric Algebra 2D Problems 2
• Geometric Algebra 2D Problems 3
• Geometric Algebra 1D

Gleichungen

Äquivalenzumformungen mit dem CAS untersuchen

Unterrichtsidee: Äquivalenzumformungen untersuchen in Klasse 8 (aus CAS-Fortbildung)

Äquivalenzumformungen werden am Anfang meist eingeführt als einfache Anweisungen, wie man eine Gleichung "umbaut". Dabei macht man sich gerne das Waagenmodell zunutze.

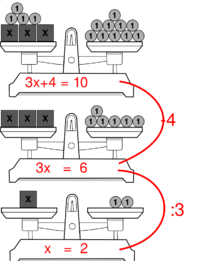
Entsprechend der Idee von Prof. Dr. Regina Bruder von der TU Darmstadt, die kann man dann erst einmal den Umgang mit Äquivalenzumformungen üben, indem man die Aufgabengrundidee variiert (Erklärungen dazu hier in Tabelle 1 Seite 6/7):

• Äquivalenzumformungen vorgeben und anwenden lassen.
• Äquivalenzumformungen erkennen lassen, wenn zwei Gleichungen vorgegeben sind.
• Vorherige Gleichung bestimmen lassen, wenn die Äquivalenzumformungen und die folgende Gleichung gegeben ist.
• Einfache Gleichungen vorgeben, zu denen man die Lösung mit einer Äquivalenzumformung bestimmen kann.
• Äquivalenzumformungen und die umgeformte Gleichung vorgeben und fragen, ob es richtig durchgeführt wurde

Dann wird für einfache Gleichungen der Art 4x - 6 = 8 ein Verfahren vorgegeben, das man einübt. Das kann mit Aufgaben aus dem Buch geschehen oder man nutzt kleine GeoGebra-Apps, die auch am Handy ein einüben dieses Schemas erlauben.

<iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/2029891/width/786/height/368/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/preferhtml5" width="786px" height="368px" style="border:0px;"> </iframe>

Kurzlink und QR-Code für's Smartphone: http://goo.gl/GPR09r

Im nächsten Schritt gilt es aber, sich von diesem starren Schema sich zu lösen und zu lernen, wie man beliebigen Gleichungen umgehen kann und welche Äquivalenzumformung wann mehr Sinn macht. Außerdem muss ein Verständnis dafür entwickelt werden, wie sich die Umformungen auf die Gleichungen auswirken, wie etwa die typischen Fehler beim Teilen vermieden werden.

Dazu könnte das GeoGebra-CAS verwendet werden! Meine Ideen zur Vorgehensweise dazu sind die folgenden:

• Einführung in die Nutzung des CAS (Rechnungen, Lösungen von Gleichungen bestimmen lassen, Lösungen kontrollieren durch Ersetzen von Werten)
• Term-Umformungen üben um x zu isolieren
• Vorgebene Äquivalenzumformungen im CAS anwenden und erkennen, woher das Ergebnis kommt.

Hintergedanken:

• Das GeoGebra-CAS soll bei den Schülern als Hilfsmittel zur Kontrolle ihrer Aufgaben vorgestellt werden.
• Statt nur Schematas vorzugeben, sollen die Schüler Äquivalenzumformungen ausprobieren können, auch wenn sie nicht so sinnvoll sind. Das CAS zeigt das richtige Ergebnis, die Schüler sollen dann verstehen, warum es so herauskommt.

Arbeitsauftrag Gehen Sie das Material auf der Unterseite durch und überlegen, wo es Probleme geben kann? Sehen Sie Vorteile bei dieser Vorgehensweise oder haben weitere Ideen?

Tipp: Auf sehr spielerische Art und Weise, die auch schon für Grundschul- und sogar Kindergartenkinder geeignet ist, führt das App DragonBox Algebra 12+ in das Lösen von Gleichungen ein. Hier wird Algebra geübt, ohne das das Kind es merkt. Bei Interesse können Sie das App bei mir ausprobieren. Playstore, iTunes, Produkt-Trailer , Vorstellungs-Video