GPS im Mathematikunterricht
Satelliten weisen den Weg
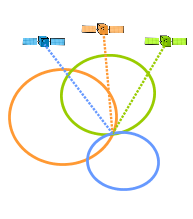
Wie funktioniert das GPS ?
Dieses Thema eignet sich gut zum Recherchieren und Präsentieren, da Internet ausreichend viele Informationen über die Funktionsweise vom GPS stehen.
Hier nur zwei exemplarische Beispiele:
- Planet Schule: Satelliten weisen den Weg. Die Filme von Planet Schule dürfen heruntergeladen, weitergegeben und für schulische zwecke genutzt werden.
- Wie funktioniert das GPS-System? Eine Video vom YouTube. Die Videos vom YouTube dürfen in der Regel nicht heruntergeladen (YouTube-Standardlizenz) aber live angeschaut werden.
Was bedeuten die Zahlen?
Beispiel: Mainz 50°0'Nord, 8°16'Ost
Dies bedeutet: λ=8°16' und Φ=50°0'
λ wird auch "longitude" und Φ "latitude" genannt.
Der "Nullpunkt" mit 0°N, 0°O findet man auf dem Equator im Atlantischen Ozean "links neben Afrika".
Wie können die Koordinaten bestimmt werden?
- Mit einem GPS-Empfänger (GPS-Empfänger können bei den Medienzentren ausgeliehen werden.)
- Mit einem Smatphone und einem passenden App.
- Aus dem Internet durch suchen: Suchen Sie nach konkreten Koordinaten (geben Sie in eine Suchmaschine z.B. 50°0'N 8°16'E ein).
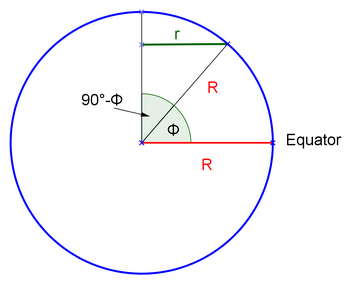
Geometrie in der Sek I
Erdradius und Länge vom Breitengrad bestimmen.
| Schritt | Wie ? | Beispiel: Speyer (Altpörtel-Dom) |
|---|---|---|
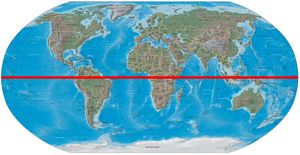
| 1 | Suchen Sie zwei Punkte, deren Verbindungslinie genau parallel zur Äquator verläuft. Dies erkennen Sie daran, dass die "Nord-Koordinaten" der beiden Punkte gleich sind: |
Altpörtel: 49° 19' 3.00 N 8° 25' 56.82 E Dom: 49° 19' 3.00 N 8° 26' 28.82 E |
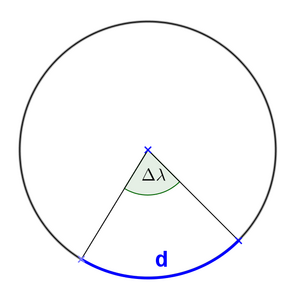
| 2 | Bestimmen Sie die Differenz der "Ost-Koordinaten": <math>\mathrm{\Delta }\mathrm{\lambda }={\mathrm{\lambda }}_{1}-{\mathrm{\lambda }}_{2}</math> |
<math>\mathrm{\Delta }\mathrm{\lambda }</math> = 32" = 0,0089° |
| 3 | Bestimmen Sie die Entfernung der beiden Punkten. Dies kann durch messen, durch Aufzeichnen der Strecke (Smartphone) oder, |
d = 647 m |
| 4 | Berechnen Sie den Umfang des Breitengrades. |
<math>\mathrm{\Delta }\mathrm{\lambda }</math> →647 m 360° → U |
| 5 | Jetzt kann erst der Radius des Breitengrades (r), dann der Erdradius (R) bestimmt werden. |
U=26203,5km = 2r <math>\mathrm{\pi}</math> <math>\Rightarrow</math> r = 4170,4 km |
Wenn die Messung auf dem Schulhof erfolgt ist die gemessene Strecke zwischen den beiden Punkten deutlich geringer. Dies verursacht eine hohe Messungenauigkeit und das Ergebnis wird nicht so gut, wie hier im Beispiel sein.
In diesem Fall lohnt es sich die Aufgabe als Hausaufgabe zu wiederholen, wobei die "Messwerte" diesmal anhand von Internetrecherche ermittelt werden sollen (oder von Ihnen vorgegeben werden sollen).
Bezug zum Medienkomp@ss
- Bei diesem Unterrichtseinheit kann die Funktionsweise der Navigationssysteme erkundet werden.
- Es gibt viele Anlässe zu Recherchieren, Analysieren und Reflektieren.
- Neben den oben angeführten Themen kann nach den Berechnungen auch über die
- * Genauigkeit von Navigationssysteme oder
- * über die Schlagzeile: "KFZ-Versicherungen planen fahrstilbasierte Tarife" diskutiert werden.
- (Stellen Sie sich vor: Sie fahren auf dem Autobahn mit einem Geschwindigkeit von 130 km/h. Parallel, dicht neben dem Autobahn verläuft einige Hundert Meter lang ein Fahrradweg. Ihr Navigationssystem zeichnet Ihre Strecke fälschlicher weise so auf, als ob Sie auf dem Fahrradweg fahren würden.)
Funktionen und Diagramme in der Sek I
Analyse vom Selbst aufgenommenen GPS-Tracks - oder: Funktionen erzählen wahre Geschichten
Es gibt unzählige Apps für Smartphones, mit denen die eigene Route aufgezeichnet werden kann. Ich habe probeweise einen kurzen Fahrradweg aufgezeichnet:
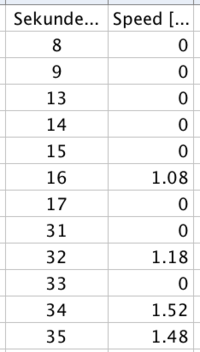
Mein App lieferte
- Messdaten (Geschwindigkeit, Entfernung, GPS-Koordinaten in 1-2 Sekundentakt aufgenommen) als cvs-Datei. Diese Datei kann leicht in eine Tabelle umgewandelt werden.
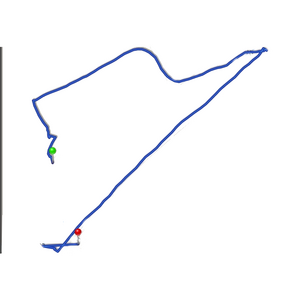
- Einen Kartenausschnitt, auf dem mein Weg eingezeichnet war.
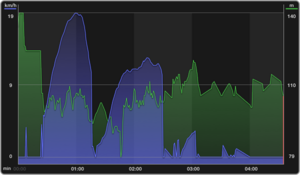
- Ein Histogramm über meine Geschwindigkeit, Entfernung und Steigung.
Diese Darstellungsformen können gut miteinander verglichen werden. Es können dabei auch folgende Fragen gestellt werden:
- Welche Streckenpunkte können im Histogramm identifiziert werden?
- Wo habe ich mich beschleunigt, wo bin ich stehengeblieben, wo wurde ich langsamer?
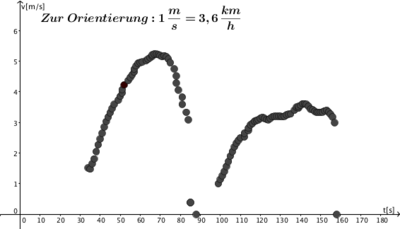
Um die Bearbeitungsmöglichkeiten zu erweitern habe ich die Daten in GeoGebra übertragen:
So können weitere Fragen gestellt werden:
- Welche Funktionen beschreiben die einzelnen Abschnitte am Besten?
- Kann mann - und wenn ja, wie - die Entfernung anhand des Zeit-Geschwindigkeit-Diagramms bestimmen?
Analysis in der Sek II
Einführung in die Differential- und Integralrechnung.
Weiteres Material
Interessante Ideen finden Sie auf den Seiten von Dr. Wolfgang Riemer.