3 - Bezierkurven und Bernsteinpolynome
Bernsteinpolynome
Der Erfinder: Joseph Bernstein
"Joseph Naumowitsch Bernstein (... * 18. April 1945 in Moskau) ist ein in Russland geborener israelischer Mathematiker, der sich mit Darstellungstheorie, algebraischer Geometrie, automorphen Funktionen und Zahlentheorie beschäftigt.
Bernstein studierte an der Universität Moskau ab 1963, machte dort 1968 sein Diplom und wurde 1972 bei Israel Gelfand promoviert. 1981/82 war er Gastprofessor an der University of Maryland und von 1983 bis 1993 Professor in Harvard. Ab 1993 war er Professor an der Universität Tel Aviv."
Bezierkurven als Parameterkurven
Geometrische Konstruktionen sind schwer weiterzubearbeiten. Es ist günstiger, wenn die Kurven als Funktionen zur Verfügung stehen.
Es gibt zwar keine Funktion, die eine Bezierkurve beschreibt, die Koordinaten der Punkte erfüllen aber durchaus bestimmte Mathematische Gesätze. Als Grundlage brauchen wir dazu drei Bernsteinpolynome:
- B03(x) = -x³+3x²-3x+1
- B13(x) = 3x³-6x-2+3x
- B23(x) = -3x³+3x²
- B33(x) = x³
Konstruktion:
| Schritt | Was ? | Wo? | Wie? |
|---|---|---|---|
| 1 | Markieren Sie vier Punkte. im Grafik-Ansicht. | Grafik-Ansicht | |
| 2 | Definieren Sie einen Schieberegler t | 0 ≤ t ≤ 1, Schrittweite:0,01 | |
| 3 | Definieren Sie die Funktionen, die später die x- und y-Koordinaten vom Punkt P steuern werden. | Eingabezeile | PX(t)=x(A)*B03(t)+x(B)*B13(t)+x(C)*B23(t)+x(D)*B33(t) und PY(t)=y(A)*B03(t)+y(B)*B13(t)+y(C)*B23(t)+y(D)*B33(t) |
| 3 | Definieren Sie Punkt P | Eingabezeile | PY(t) |
| 4 | Starten Sie die Animation von t | ||
| 5 | Zeichnen Sie die Ortslinie von P | Eingabezeile | Ortslinie[P,t] |
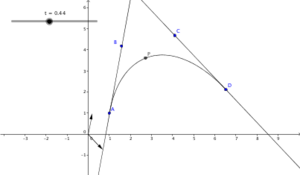
Sie Haben nun eine perfekte Bezierkurve erhalten. Sie können die Form der Kurve verändern, wenn Sie die Punkte A, B, C und D bewegen.
P sitzt in A, wenn t = 0 und in B, wenn t = 1 ist.
Ableitungen und Tangenten
Parameterkurven können Koordinatenweise abgeleitet werden.
- Leiten Sie die Funktionen PX und PY mit dem Befehl Ableiteung ab.
- Definieren Sie einen Vektor <math>\vec v</math> mit den Koordinaten (PX'(0)|PY'(0)). So haben Sie die Ableitung der Bezierkurve im Punkt A erstellt.
- Zeichnen Sie eine Gerade durch A, parallel zu <math>\vec v</math>. Diese Gerade ist die Tangente zur Kurve durch A.
- Erstellen Sie ähnliche Weise die Tangente durch Punkt D.
Es ist gut zu erkennen, dass die Tangenten immer durch B bzw. durch C laufen.
Die dritte Dimension kommt dazu
Sie können die oben beschriebene Konstruktion auch im dreidimensionalen Raum erstellen: Sie müssen allerdings alle Punkte von Anfang an mit drei Koordinaten anlegen.
Die dritte Koordinate von P wird analog zu den ersten beiden Koordinaten definiert.