Teil 1: Einführung in GeoGebra CAS

Fortbildung GeoGebra CAS:  Hauptseite Fortbildung - Hauptseite Screencasts - Teil 1: Einführung in GeoGebra CAS - Teil 2: Einsatz von GeoGebra CAS im Mathematikunterricht am Beispiel "Lineare Gleichungssysteme" - Teil 3: Vorteile und Einsatz von GeoGebra CAS im Mathematikunterricht

In diesem Teil der Fortbildung geht es darum, wichtige Eigenschaften und Funktionen von GeoGebra CAS kennenzulernen und anwenden zu können. Dazu findet man auf der Seite Lehr- und Lernvideos Screencasts und Erklärungen zu den verschiedenen Anwendungsmöglichkeiten von GeoGebra CAS.

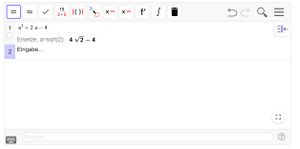
Aufgabe Nr. 1: Belegung von Variablen

Teillösung von Aufgabe 1: Belegung der Variablen mit Hilfe des dafür vorgesehenen Werkzeugs

Öffnen Sie das dynamische Arbeitsblatt.

1. Weisen Sie der Variablen a auf zwei verschiedene Arten den Wert √2 zu
2. Berechnen Sie den daraus resultierenden Wert des Terms exakt und näherungsweise
   
   

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencast "Belegung von Variablen in GeoGebra CAS"
Screencast "Die Werkzeugleiste in GeoGebra CAS"

Aufgabe Nr. 2: Umformung und Lösung von Gleichungen

Definieren Sie selbst eine geeignete Gleichung in GeoGebra CAS, die numerisch und exakt gelöst werden soll.

1. Durch Gleichungsumformung
2. Mit Hilfe der Werkzeugleiste
   
   

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencast "Gleichungen in GeoGebra CAS"
Screencast "Die Werkzeugleiste in GeoGebra CAS"

Aufgabe Nr. 3: Funktionen

Definieren Sie eine beliebige Funktion in GeoGebra CAS und berechnen Sie näherungsweise und exakt die Funktionswerte an den Stellen x=-2, x=√3 und x=e

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencast "Funktionen in GeoGebra CAS"
Screencast "Die Werkzeugleiste in GeoGebra CAS"

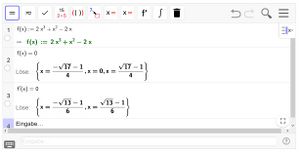
Aufgabe Nr. 4: Elemente der Kurvendiskussion 1

Definieren Sie eine beliebige Funktion dritten Grades in GeoGebra CAS. Bestimmen Sie danach

1. die Ableitung und eine Stammfunktion dieser Funktion.
2. die Steigung dieser Funktion an der Stelle x=2.
3. die Extrempunkte dieser Funktion.
   
   

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencast "Funktionen in GeoGebra CAS"
Screencast "Die Werkzeugleiste in GeoGebra CAS"
Screencast "Gleichungen in GeoGebra CAS"

Aufgabe Nr. 5: Definieren und lösen eines linearen Gleichungssystems

Definieren Sie ein lineares Gleichungssystem in GeoGebra CAS. Das lineare Gleichungssystem sollte maximal drei Variablen enthalten, die Anzahl der Gleichungen ist beliebig. Bestimmen Sie die Lösungsmenge dieses linearen Gleichungssystems.

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencasts "Lineare Gleichungssysteme und deren geometrische Interpretation in GeoGebra CAS"

Aufgabe Nr. 6: Elemente der Kurvendiskussion 2

Teillösung von Aufgabe 6, Teil a und b: Bestimmung der Nullstellen von f(x) und f'(x)

Öffnen Sie das dynamische Arbeitsblatt.

1. Bestimmen Sie exakt und näherungsweise die Schnittpunkte der Funktionen f(x), g(x) und h(x) mit den Koordinatenachsen.
2. Bestimmen Sie exakt und näherungsweise die Koordinaten der Extrem- und Wendepunkte der gegebenen Funktionen f(x), g(x) und h(x).
3. Bestimmen Sie exakt und näherungsweise diejenigen Stellen, an welchen die Steigung der Funktionen f(x), g(x) und h(x) mit ihrem y-Wert übereinstimmt.
   
   

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencast "Funktionen in GeoGebra CAS"
Screencast "Die Werkzeugleiste in GeoGebra CAS"
Screencast "Gleichungen in GeoGebra CAS"

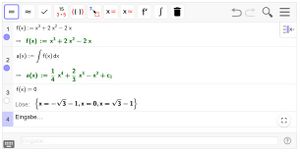
Aufgabe Nr. 7: Integralrechnung 1

Teillösung von Aufgabe 7: Bildung einer Stammfunktion von f(x) und Bestimmung der Nullstellen von f(x)

Öffnen Sie das dynamische Arbeitsblatt.

Bestimmen Sie die Größe der Fläche, die die Funktion f(x) mit der x-Achse einschließt.

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencast "Funktionen in GeoGebra CAS"
Screencast "Die Werkzeugleiste in GeoGebra CAS"

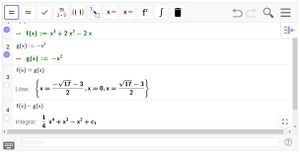
Aufgabe Nr. 8: Integralrechnung 2

Teillösung zu Aufgabe 8: Bestimmung der Schnittpunkte von f(x) und g(x) und Bestimmung einer Stammfuktion von f(x)-g(x)

Öffnen Sie das dynamische Arbeitsblatt.

Bestimmen Sie die Größe der Fläche, die von den Funktionen f(x) und g(x) eingeschlossen wird.

Zur Bearbeitung dieser Aufgabe sind folgende Screencasts hilfreich:

Screencast "Funktionen in GeoGebra CAS"
Screencast "Die Werkzeugleiste in GeoGebra CAS"