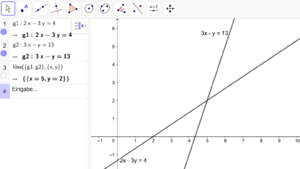
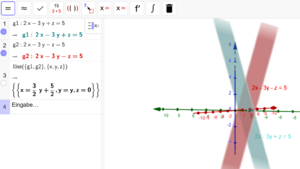
Teil 2: Einsatz von GeoGebra CAS im Mathematikunterricht am Beispiel "Lineare Gleichungssysteme"
Im zweiten Teil der Fortbildung geht es um den beispielhaften Einsatz von GeoGebra CAS im Mathematikunterricht. Dies geschieht am Beispiel des Themas "Lineare Gleichungssysteme". Wie man lineare Gleichungssysteme allgemein lösen kann und wie man die Lösungsmenge verschiedener linearer Gleichungssysteme geometrisch interpretieren kann wird in verschiedenen Screencasts "Lineare Gleichungssysteme und deren geometrische Interpretation in GeoGebra CAS" erklärt.
Zur Bearbeitung aller Aufgaben sind folgende Screencasts hilfreich:
Screencasts "Lineare Gleichungssysteme und deren geometrische Interpretation in GeoGebra CAS"
Screencast "Einführung in das 3D-Fenster"
Lineare Gleichungssysteme mit zwei Variablen
Aufgabe Nr. 1: Definiton und Lösung eines linearen Gleichungssystems und geometrische Interpretation im Grafik-Fenster
Definieren Sie ein beliebiges lineares Gleichungssystem mit zwei Gleichungen und zwei Variablen in GeoGebra CAS und lösen sie dieses. Interpretieren Sie das Gleichungssystem und dessen Lösungsmenge geometrisch und überprüfen Sie ihre Lösung mit Hilfe des Grafik-Fensters.
Aufgabe Nr. 2: Lösung eines linearen Gleichungssystems und geometrische Interpretation im Grafik-Fenster
Öffnen Sie das dynamische Arbeitsblatt.
Bestimmen Sie die Lösungsmenge des linearen Gleichungssystems mit GeoGebra CAS und interpretiere Sie das Gleichungssystem und seine Lösungsmenge geometrisch. Überprüfen Sie Ihr Ergebnis mit Hilfe des Grafik-Fensters.
Aufgabe Nr. 3: Algebraische Interpretation der geometrischen Ansicht eines linearen Gleichungssystems im Grafik-Fenster
Öffnen Sie das dynamische Arbeitsblatt.
Betrachten Sie die Geraden im Grafik-Fenster. Welche Art der Lösungsmenge würde im CAS-Fenster angezeigt, wenn man die drei Geraden als Gleichungen eines linearen Gleichungssystems auffassen und dieses lösen würde? Öffnen Sie das CAS-Fester und prüfen Sie Ihre Annahme.
Lineare Gleichungssysteme mit drei Variablen
Aufgabe Nr. 4: Lösung eines linearen Gleichungssystems und geometrische Interpretation im 3D-Fenster 1
Öffnen Sie das dynamische Arbeitsblatt.
Bestimmen Sie die Lösungsmenge des linearen Gleichungssystems mit GeoGebra CAS und interpretieren Sie das Gleichungssystem und seine Lösungsmenge geometrisch. Überprüfen Sie Ihr Ergebnis mit Hilfe des 3D-Fensters.
Aufgabe Nr. 5: Lösung eines linearen Gleichungssystems und geometrische Interpretation im 3D-Fenster 2
Öffnen Sie das dynamische Arbeitsblatt.
Bestimmen Sie die Lösungsmenge des linearen Gleichungssystems mit GeoGebra CAS und interpretieren Sie das Gleichungssystem und seine Lösungsmenge geometrisch. Überprüfen Sie Ihr Ergebnis mit Hilfe des 3D-Fensters.
Aufgabe Nr. 6: Algebraische Interpretation der geometrischen Ansicht eines linearen Gleichungssystems im 3D-Fenster 1
Öffnen Sie das dynamische Arbeitsblatt.
Betrachten Sie die Ebenen im 3D-Fenster. Welche Art der Lösungsmenge würde im CAS-Fenster angezeigt, wenn man die drei Ebenen als Gleichungen eines linearen Gleichungssystems auffassen und dieses lösen würde? Öffnen Sie das CAS-Fester und prüfen Sie Ihre Annahme.
Aufgabe Nr. 7: Algebraische Interpretation der geometrischen Ansicht eines linearen Gleichungssystems im 3D-Fenster 2
Öffnen Sie das dynamische Arbeitsblatt.
Betrachten Sie die Ebenen im 3D-Fenster. Welche Art der Lösungsmenge würde im CAS-Fenster angezeigt, wenn man die drei Ebenen als Gleichungen eines linearen Gleichungssystems auffassen und dieses lösen würde? Öffnen Sie das CAS-Fester und prüfen Sie Ihre Annahme.
Vertiefungsaufgaben
Aufgabe Nr. 8: Veränderung der Gleichungen eines linearen Gleichungssystems mit zwei Variablen, um eine bestimmte Lösungsmenge zu erhalten
Öffnen Sie das dynamische Arbeitsblatt.
Ändern Sie die Gleichungen der Geraden im CAS-Fenster, unter Zuhilfenahme des Grafik-Festers und der Lösungsmenge, so ab,
- dass das lineare Gleichungssystem eine eindeutige Lösung besitzt.
- dass das lineare Gleichungssystem unendlich viele Lösungen besitzt.
Aufgabe Nr. 9: Veränderung der Gleichungen eines linearen Gleichungssystems mit drei Variablen, um eine bestimmte Lösungsmenge zu erhalten
Öffnen Sie das dynamische Arbeitsblatt.
Ändern Sie die Gleichungen der Ebenen im CAS-Fenster, unter Zuhilfenahme des 3D-Festers und der Lösungsmenge, so ab,
- dass das lineare Gleichungssystem eine eindeutige Lösung besitzt.
- dass das lineare Gleichungssystem eine Schnittgerade als Lösung besitzt.